题目内容
已知函数f(x)=x|x|-2x.
(1)求方程f(x)=0的解;
(2)作出函数y=f(x)的草图,并指出它的递增区间.
(1)求方程f(x)=0的解;
(2)作出函数y=f(x)的草图,并指出它的递增区间.
考点:函数图象的作法,函数单调性的判断与证明,函数的零点
专题:函数的性质及应用
分析:(1)由x|x|-2x=x(|x|-2)可得:f(x)=0,则x=0,或|x|-2=0,进而得到答案;
(2)利用零点分段法,可将函数的解析式化为:f(x)=x|x|-2x=
的形式,进而结合二次函数的图象得到答案.
(2)利用零点分段法,可将函数的解析式化为:f(x)=x|x|-2x=
|
解答:
解:(1)令f(x)=x|x|-2x=x(|x|-2)=0,
则x=0,或|x|-2=0,即x=±2,
故方程f(x)=0的解为:-2,0,2
(2)f(x)=x|x|-2x=
的图象如下图所示:
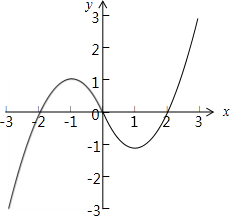
由图可得:函数y=f(x)的递增区间为:(-∞,-1],[1,+∞)
则x=0,或|x|-2=0,即x=±2,
故方程f(x)=0的解为:-2,0,2
(2)f(x)=x|x|-2x=
|
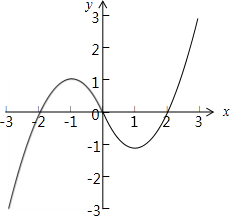
由图可得:函数y=f(x)的递增区间为:(-∞,-1],[1,+∞)
点评:本题考查的知识点是函数图象的作法,函数的单调区间,函数的零点,是函数图象和性质的综合应用,但考点比较基本,难度不大.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
设集合A={x|0<x<2},B={x|y=2sinx},则A∩B=( )
| A、{x|1≤x<2} |
| B、{x|0<x<1} |
| C、{x|0<x≤2} |
| D、{x|0<x<2} |
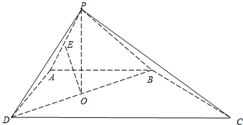 如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点.
如图,四棱锥P-ABCD的底面是直角梯形,AB∥CD,AB⊥AD,△PAB和△PAD是两个边长为2的正三角形,DC=4,O为BD的中点,E为PA的中点. 如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.
如图,三棱锥S-ABC中,侧面SAB与侧面SAC均为边长为2的正三角形,且∠BAC=90°,O、D分别为BC、AB的中点.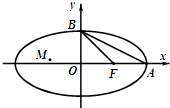 如图,椭圆C:
如图,椭圆C: