题目内容
5.抛掷两枚质地均匀的正四面体骰子,其4个面分别标有数字1,2,3,4,记每次抛掷朝下一面的数字中较大者为a(若两数相等,则取该数),平均数为b,则事件“a-b=1”发生的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
分析 基本事件总数n=4×4=16,再利用列举法求出事件“a-b=1“包含的基本事件的个数,由此能求出事件“a-b=1”发生的概率.
解答 解:抛掷两枚质地均匀的正四面体骰子,其4个面分别标有数字1,2,3,4,
记每次抛掷朝下一面的数字中较大者为a(若两数相等,则取该数),平均数为b,
基本事件总数n=4×4=16,
事件“a-b=1“包含的基本事件有:
(1,3),(3,1),(2,4),(4,2),共有4个,
∴事件“a-b=1”发生的概率为p=$\frac{4}{16}$=$\frac{1}{4}$.
故选:B.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
相关题目
15.若α是第四象限角,且$cosα=\frac{3}{5}$,则tan2α=( )
| A. | $-\frac{4}{3}$ | B. | $-\frac{24}{7}$ | C. | $\frac{24}{7}$ | D. | $\frac{24}{25}$ |
13.下列命题中的假命题是( )
| A. | log23<log35 | B. | ?x∈(-∞,0),ex>x+1 | ||
| C. | ${log_{\frac{1}{2}}}3<{(\frac{1}{2})^3}<{3^{\frac{1}{2}}}$ | D. | ?x>0,x>sinx |
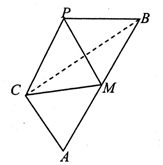 已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.
已知△ABC中,∠C=90°,tanA=$\sqrt{2}$,M为AB的中点,现将△ACM沿CM折成三棱锥P-CBM,当二面角P-CM-B大小为60°时,$\frac{AB}{PB}$=$\sqrt{3}$.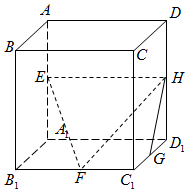 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.