题目内容
15.若α是第四象限角,且$cosα=\frac{3}{5}$,则tan2α=( )| A. | $-\frac{4}{3}$ | B. | $-\frac{24}{7}$ | C. | $\frac{24}{7}$ | D. | $\frac{24}{25}$ |
分析 由已知利用同角三角函数基本关系式可求sinα,tanα,进而利用二倍角的正切函数公式即可计算得解tan2α.
解答 解:∵α是第四象限角,且$cosα=\frac{3}{5}$,
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{4}{5}$,
∴tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$,
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×(-\frac{4}{3})}{1-(-\frac{4}{3})^{2}}$=$\frac{24}{7}$.
故选:C.
点评 本题主要考查了同角三角函数基本关系式,二倍角的正切函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
5.执行如图所示的程序框图,输出的n值为( )
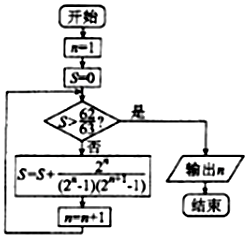

| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
6.执行如图的程序框图,则输出x的值是( )
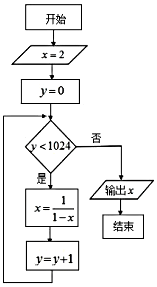

| A. | 2016 | B. | 1024 | C. | $\frac{1}{2}$ | D. | -1 |
7.已知数列{an}满足:an=$\left\{\begin{array}{l}{1,1≤n≤2016}\\{2•(\frac{1}{3})^{n-2016},n≥2017}\end{array}\right.$,设Sn表示数列{an}的前n项和.则下列结论正确的是( )
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |
5.抛掷两枚质地均匀的正四面体骰子,其4个面分别标有数字1,2,3,4,记每次抛掷朝下一面的数字中较大者为a(若两数相等,则取该数),平均数为b,则事件“a-b=1”发生的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |