题目内容
20.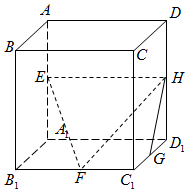 如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
如图,在正方体ABCD-A1B1C1D1中,E,F,G,H分别为棱AA1,B1C1,C1D1,DD1的中点,则GH与平面EFH所成角的余弦值为$\frac{3\sqrt{10}}{10}$.
分析 C1H,过G作GM⊥C1H于M,则∠GHC1即为GH与平面EFH所成的角,在△C1GH利用余弦定理求出cos∠GHC1.
解答 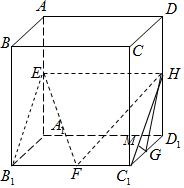 解:连结EB1,C1H,则平面EFH即为平面EHC1B1,
解:连结EB1,C1H,则平面EFH即为平面EHC1B1,
过G作GM⊥C1H于M,则MG⊥平面EFH,
∴∠GHC1即为GH与平面EFH所成的角,
设正方体棱长为2,则C1G=1,GH=$\sqrt{2}$,C1H=$\sqrt{5}$,
∴cos∠GHC1=$\frac{G{H}^{2}+{C}_{1}{H}^{2}-{C}_{1}{G}^{2}}{2GH•{C}_{1}H}$=$\frac{2+5-1}{2×\sqrt{2}×\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
故答案为$\frac{3\sqrt{10}}{10}$.
点评 本题考查了直线与平面所成角的求解,属于中档题.

练习册系列答案
相关题目
5.抛掷两枚质地均匀的正四面体骰子,其4个面分别标有数字1,2,3,4,记每次抛掷朝下一面的数字中较大者为a(若两数相等,则取该数),平均数为b,则事件“a-b=1”发生的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{8}$ |
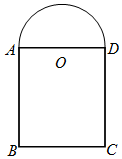 设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).
设计人员要用10米长的材料(材料的宽度不计)建造一个窗子的边框,如图所示,窗子是由一个矩形ABCD和以AD为直径的半圆组成,窗子的边框不包括矩形的AD边,设半圆的半径为OA=r(米),窗子的透光面积为S(平方米).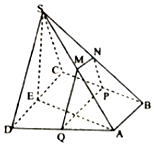 如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.
如图,四棱锥S-ABCD中,底面ABCD为直角梯形,AB∥CD,BC⊥CD,平面SCD⊥平面ABCD,SC=CD=SD=AD=2AB=2,M,N分别为SA,SB的中点,E为CD的中点,过M,N作平面MNPQ分别与交BC,AD于点P,Q.