题目内容
17.探究函数f(x)=2x+$\frac{8}{x}$,x∈(0,+∞)最小值,并确定取得最小值时x的值.列表如下:| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 17 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)上递减;函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(2,+∞)上递增.当x=2时,y最小=8.
(2)证明:函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+$\frac{8}{x}$(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
分析 (1)根据表格可求得函数的单调区间,根据单调性可求得最小值;
(2)利用单调性的定义可作出证明;
(3)根据奇函数的性质可作出回答.
解答 解:(1)f(x)在(2,+∞)递增;当x=2时,y取得最小值8.
故答案为:(2,+∞),2,8.
(2)证明:设x1,x2是区间(0,2)上的任意两个数,且x1<x2,
f(x1)-f(x2)=2x1+$\frac{8}{{x}_{1}}$-(2x2+$\frac{8}{{x}_{2}}$)=2(x1-x2)+8($\frac{1}{{x}_{1}}$-$\frac{1}{{x}_{2}}$)
=2(x1-x2)(1-$\frac{4}{{x}_{1}{x}_{2}}$)=$\frac{2({x}_{1}-{x}_{2})({x}_{1}{x}_{2}-4)}{{x}_{1}{x}_{2}}$,
由x1<x2,可知x1-x2<0,
又x1,x2∈(0,2),可知0<x1x2<4,即x1x2-4<0,则f(x1)-f(x2)>0,
故函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减;
(3)函数f(x)=2x+$\frac{8}{x}$在(-∞,0)时,当x=-2时,有最大值-8.
点评 本题考查函数单调性的性质及其证明,同时考查奇函数的性质:最值相反,属基础题.

练习册系列答案
相关题目
2.设Sn是等比数列{an}的前n项和,S4=5S2,则此数列的公比q=( )
| A. | -2或-1 | B. | 1或2 | C. | ±1或2 | D. | ±2或-1 |
6.在等差数列46,43,40,37,…中第一个负数项是( )
| A. | 第15项 | B. | 第16项 | C. | 第17项 | D. | 第18项 |
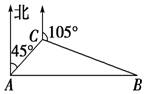 一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.
一商船行至索马里海域时,遭到海盗的追击,随即发出求救信号.正在该海域执行护航任务的海军“黄山”舰在A处获悉后,即测出该商船在方位角为45°距离10海里的C处,并沿方位角为105°的方向,以9海里/时的速度航行.“黄山”舰立即以21海里/时的速度前去营救.如图所示,求“黄山”舰靠近商船所需要的最少时间及所经过的路程.