题目内容
5.设点M(x1,f(x1))和点N(x2,g(x2))分别是函数f(x)=ex-$\frac{1}{2}$x2和g(x)=x-1图象上的点,且x1≥0,x2>0,若直线MN∥x轴,则M,N两点间的距离的最小值为2.分析 求出导函数f′(x),根据题意可知f(x1)=g(x2),令h(x)=ex-$\frac{1}{2}$x2+1-x(x≥0),求出其导函数,进而求得h(x)的最小值即为M、N两点间的最短距离.
解答 解:∵当x≥0时,f'(x)=ex-x>0,∴函数y=f(x)在[0,+∞)上单调递增.
∵点M(x1,f(x1))和点N(x2,g(x2))分别是函数f(x)=ex-$\frac{1}{2}$x2和g(x)=x-1图象上的点,
且x1≥0,x2>0,若直线MN∥x轴,则f(x1)=g(x2),即${e}^{{x}_{1}}-\frac{1}{2}{{x}_{1}}^{2}$=x2-1,
则M,N两点间的距离为x2-x1=${e}^{{x}_{1}}-\frac{1}{2}{{x}_{1}}^{2}$+1-x1.
令h(x)=ex-$\frac{1}{2}$x2+1-x,x≥0,则h′(x)=ex-x-1,h″(x)=ex-1≥0,
故h′(x)在[0,+∞)上单调递增,故h′(x)=ex-x-1≥h′(0)=0,
故h(x)在[0,+∞)上单调递增,故h(x)的最小值为h(0)=1-0+1-0=2,
即M,N两点间的距离的最小值为2,
故答案为2.
点评 本题主要考查了利用函数的导数求出函数的单调性以及函数的极值问题,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
20.过点P(1,1)作直线l,与两坐标轴相交所得三角形面积为4,则直线l有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
20.已知cos(α+$\frac{π}{4}}$)=$\frac{3}{5}$,$\frac{π}{2}$≤α<$\frac{3π}{2}$,则sin2α=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{7}{25}$ | D. | $\frac{7}{25}$ |
10.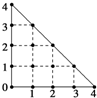 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
这里,两株作物“相近”是指它们之间的直线距离不超过1米.
(1)完成下表,并求所种作物的平均年收获量:
(2)在所种年收获量为51或48的作物中随机选取两株求收获量之和,收获量之和为t的概率.
 某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:
某人在如图所示的直角边长为4米的三角形地块的每个格点(指纵、横直线的交叉点以及三角形的顶点)处都种了一株相同品种的作物.根据历年的种植经验,一株该种作物的年收获量Y(单位:kg)与它的“相近”作物株数X之间的关系如表所示:| X | 1 | 2 | 3 | 4 |
| Y | 51 | 48 | 45 | 42 |
(1)完成下表,并求所种作物的平均年收获量:
| Y | 51 | 48 | 45 | 42 |
| 频数 |
17.探究函数f(x)=2x+$\frac{8}{x}$,x∈(0,+∞)最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)上递减;函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(2,+∞)上递增.当x=2时,y最小=8.
(2)证明:函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+$\frac{8}{x}$(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 17 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)上递减;函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(2,+∞)上递增.当x=2时,y最小=8.
(2)证明:函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+$\frac{8}{x}$(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
15.已知集合M={x|mx2+2x+m=0,m∈R]中有且只有一个元素的所有m的值组成的集合为N,则N为( )
| A. | {-1,1} | B. | {0,1] | C. | {-1,0,1} | D. | N⊆{-2,-1,0,2} |

