题目内容
12.若-$\frac{π}{2}$<a<$\frac{π}{2}$,sinα=$\frac{3}{5}$,则cot2α=$\frac{7}{24}$.分析 根据α的取值范围求得cosα=$\frac{4}{5}$,由同角三角函数关系得到tanα=$\frac{3}{4}$,结合倍角公式进行解答.
解答 解:∵-$\frac{π}{2}$<a<$\frac{π}{2}$,sinα=$\frac{3}{5}$,
∴cosα=$\frac{4}{5}$,
∴tanα=$\frac{3}{4}$,
∴tan2α=$\frac{2tanα}{1-ta{n}^{2}α}$=$\frac{2×\frac{3}{4}}{1-(\frac{3}{4})^{2}}$=$\frac{24}{7}$,
∴cot2α=$\frac{1}{tan2α}$=$\frac{7}{24}$.
故答案是:$\frac{7}{24}$.
点评 本题主要考察了同角三角函数关系式和二倍角的应用,属于基本知识的考查.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
3.已知某几何体的三视图如图所示,则这个几何体的体积为( )


| A. | 12π | B. | 45π | C. | 57π | D. | 24π |
20.过点P(1,1)作直线l,与两坐标轴相交所得三角形面积为4,则直线l有( )
| A. | 1条 | B. | 2条 | C. | 3条 | D. | 4条 |
7.若$\overrightarrow{a}$与$\overrightarrow{b}$-$\overrightarrow{c}$都是非零向量,则“$\overrightarrow{a}$•$\overrightarrow{b}$=$\overrightarrow{a}$•$\overrightarrow{c}$”是“$\overrightarrow{a}$⊥($\overrightarrow{b}$-$\overrightarrow{c}$)”的( )
| A. | 充分但非必要条件 | B. | 必要但非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
17.探究函数f(x)=2x+$\frac{8}{x}$,x∈(0,+∞)最小值,并确定取得最小值时x的值.列表如下:
请观察表中y值随x值变化的特点,完成以下的问题.
(1)函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)上递减;函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(2,+∞)上递增.当x=2时,y最小=8.
(2)证明:函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+$\frac{8}{x}$(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
| x | … | 0.5 | 1 | 1.5 | 1.7 | 1.9 | 2 | 2.1 | 2.2 | 2.3 | 3 | 4 | 5 | 7 | … |
| y | … | 17 | 10 | 8.34 | 8.1 | 8.01 | 8 | 8.01 | 8.04 | 8.08 | 8.6 | 10 | 11.6 | 15.14 | … |
(1)函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)上递减;函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(2,+∞)上递增.当x=2时,y最小=8.
(2)证明:函数f(x)=2x+$\frac{8}{x}$(x>0)在区间(0,2)递减.
(3)思考:函数f(x)=2x+$\frac{8}{x}$(x<0)时,有最值吗?是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
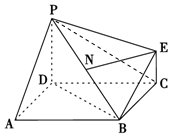 如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.
如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.