题目内容
定义在R上的函数f(x)是增函数,且对任意的x恒有f(x)=-f(2-x),若实数a,b满足不等式组
,则a2+b2的范围为( )
|
| A、[13,27] |
| B、[25,45] |
| C、[13,45] |
| D、[13,49] |
考点:函数恒成立问题
专题:函数的性质及应用
分析:由函数的性质可化原不等式组为
,a2+b2表示点(a,b)到点(0,0)的距离的平方,数相结合可得答案.
|
解答:
解:∵f(x)=-f(2-x),∴-f(x)=f(2-x),
∴f(a2-6a+23)+f(b2-8b)≤0可化为f(a2-6a+23)≤-f(b2-8b)=f(2-b2+8b),
又∵f(x)在R上单调递增,∴a2-6a+23≤2-b2+8b,
即a2-6a+23+b2-8b-2≤0,配方可得(a-3)2+(b-4)2≤4,
∴原不等式组可化为
,
如图,点(a,b)所对应的区域为以(3,4)为圆心,2为半径的右半圆(含边界),
易知a2+b2表示点(a,b)到点(0,0)的距离的平方,
由图易知:|OA|2≤a2+b2≤|OB|2,可得点A(3,2),B(3,6)
∴|OA|2=32+22=13,|OB|2=32+62=45,
∴13≤m2+n2≤45,即m2+n2的取值范围为[13,45].
故选:C

∴f(a2-6a+23)+f(b2-8b)≤0可化为f(a2-6a+23)≤-f(b2-8b)=f(2-b2+8b),
又∵f(x)在R上单调递增,∴a2-6a+23≤2-b2+8b,
即a2-6a+23+b2-8b-2≤0,配方可得(a-3)2+(b-4)2≤4,
∴原不等式组可化为
|
如图,点(a,b)所对应的区域为以(3,4)为圆心,2为半径的右半圆(含边界),
易知a2+b2表示点(a,b)到点(0,0)的距离的平方,
由图易知:|OA|2≤a2+b2≤|OB|2,可得点A(3,2),B(3,6)
∴|OA|2=32+22=13,|OB|2=32+62=45,
∴13≤m2+n2≤45,即m2+n2的取值范围为[13,45].
故选:C

点评:本题考查函数恒成立问题,考查数形结合思想,考查学生分析问题解决问题的能力,属中档题.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
已知幂函数f(x)=x m2-2m-3(m∈Z)为偶函数,且在(0,+∞)上是单调递减函数,则m的值为( )
| A、0、1、2 | B、0、2 |
| C、1、2 | D、1 |
 如图,过椭圆C:
如图,过椭圆C: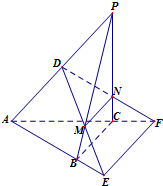 如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.
如图,在三棱锥P-ABC中,CP,CA,CB两两垂直且相等,过PA的中点D作平面α∥BC,且α分别交PB,PC于M,N,交AB,AC的延长线于E,F.