题目内容
9.在直角坐标系中,定义两点A(x1,y1),B(x2,y2)之间的“直角距离”为d(A,B)=|x1-x2|+|y1-y2|.现有以下命题:
①若A,B是x轴上两点,则d(A,B)=|x1-x2|;
②已知点A(1,2),点B在线段x+y=1(x∈[0,1])上,则d(A,B)为定值;
③已知点A(2,1),点B在椭圆$\frac{{x}^{2}}{3}$+y2=1上,则d(A,B)的取值范围是(1,5);
④若|AB|表示A,B两点间的距离,那么|AB|≥$\frac{\sqrt{2}}{2}$d(A,B).
其中真命题的是①②③④(写出所有真命题的序号)
分析 ①根据题意,可得y1=y2=0,根据定义直接判断;
②利用定义可得出d(A,B)=|1-x|+|1+x|,利用x的范围去绝对值可得结论;
③利用换元法得出则d(A,B)=3-2sin(θ+$\frac{π}{6}$),进而求出d的范围;
④根据均值定理公式ab≤${(\frac{a+b}{2})}^{2}$,结合定义和距离的内在关系得出结论.
解答 解:①若A,B是x轴上两点,
∴y1=y2=0,则d(A,B)=|x1-x2|,故正确;
②已知点A(1,2),点B在线段x+y=1(x∈[0,1])上,则d(A,B)=|1-x|+|1+x|=2,故正确;
③已知点A(2,1),点B在椭圆$\frac{{x}^{2}}{3}$+y2=1上,
∴设x=$\sqrt{3}$sinθ,则y=cosθ,
则d(A,B)=3-2sin(θ+$\frac{π}{6}$),故d的取值范围是(1,5),故正确;
④若|AB|表示A,B两点间的距离,
设a=|x1-x2|,b=|y1-y2|,
∴ab≤${(\frac{a+b}{2})}^{2}$,d2=a2+b2+2ab,
∴d2-a2-b2=2ab≤${(\frac{d}{2})}^{2}$,
∴|AB|≥$\frac{\sqrt{2}}{2}$d(A,B),故正确.
故答案为:①②③④.
点评 考查了对新定义类型题的理解和利用学过的直接解决问题的能力.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
4.设a,b∈R,且b>1是“a+b>2”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
14.将函数f(x)=sin(2x+$\frac{π}{6}$)图象上所有点向右平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则y=g(x)的图象的一条对称轴是直线( )
| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{2π}{3}$ |
1.如图,为一个半圆柱和一个半圆锥拼接而成的组合体的三视图,则该组合体的体积为( )
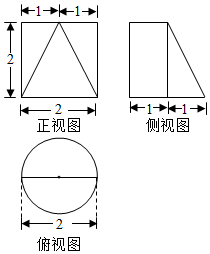

| A. | $\frac{8π}{3}$ | B. | $\frac{4π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{3}$ |
18.设集合M={x|x2-11x+10=0},N={y|y=lgx,x∈M},则M∩N=( )
| A. | {0,1} | B. | {0,1,10} | C. | {1} | D. | ∅ |
19.抛物线x2=-2y的焦点坐标为( )
| A. | $(0,-\frac{1}{8})$ | B. | $(-\frac{1}{8},0)$ | C. | $(0,-\frac{1}{2})$ | D. | $(-\frac{1}{2},0)$ |
 如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.
如图,E、F、G、H分别是空间四边形ABCD的边AB、BC、CD、DA上的点如果四边形EFGH为平行四边形,求证:AC∥平面EFGH.