题目内容

18．设集合M={x|x2-11x+10=0}，N={y|y=lgx，x∈M}，则M∩N=（　　）
A．{0，1}B．{0，1，10}C．{1}D．∅

分析 求出M中方程的解确定出M，求出N中y的值确定出N，找出两集合的交集即可．

解答 解：由M中方程变形得：（x-1）（x-10）=0，
解得：x=1或x=10，即M={1，10}，
由N中y=lgx，x∈M，得到y=0，1，即N={0，1}，
则M∩N={1}，
故选：C．

点评 此题考查了交集及其运算，熟练掌握交集的定义是解本题的关键．

练习册系列答案
相关题目
8．若如图所示的程序框图输出的S是126，则条件①可以为（　　）
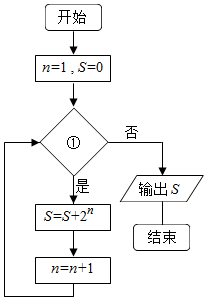
A．n≤5B．n≤6C．n≤7D．n≤8
9．在直角坐标系中，定义两点A（x1，y1），B（x2，y2）之间的“直角距离”为d（A，B）=|x1-x2|+|y1-y2|．
现有以下命题：
①若A，B是x轴上两点，则d（A，B）=|x1-x2|；
②已知点A（1，2），点B在线段x+y=1（x∈[0，1]）上，则d（A，B）为定值；
③已知点A（2，1），点B在椭圆$\frac{{x}^{2}}{3}$+y2=1上，则d（A，B）的取值范围是（1，5）；
④若|AB|表示A，B两点间的距离，那么|AB|≥$\frac{\sqrt{2}}{2}$d（A，B）．
其中真命题的是①②③④（写出所有真命题的序号）
6．如图所示，在四棱锥S-ABCD中，找出并表示所有的异面直线和二面角．
13．已知定义在（-1，1）上的奇函数，在[0，1）上单调递增，则不等式f（x2）＜f（2x）解集为（0，$\frac{1}{2}$）．
3．已知复数$z=\frac{2-i}{i^3}$（其中i是虚数单位，满足i2=-1），则z的共轭复数是（　　）
A．1-2iB．1+2iC．-1-2iD．-1+2i
10．已知等比数列{an}的各项均为正数且公比大于1，前n项积为Tn，且a2a4=a3，则使得Tn＞1的n的最小值为（　　）
A．4B．5C．6D．7
7．已知集合$A=\{x|{（x-1）^2}≤\frac{3}{2}x-\frac{1}{2}，x∈R\}$，B=N，则集合A∩B的真子集个数为（　　）
A．3B．4C．7D．8
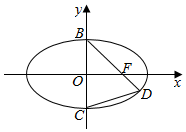8．如图，在平面直角坐标系xOy中，F为椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点，B，C分别为椭圆的上、下顶点，直线BF与椭圆的另一个交点为D，且直线CD的斜率为$\frac{1}{2}$，则该椭圆的离心率为$\frac{\sqrt{2}}{2}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网