题目内容
14.将函数f(x)=sin(2x+$\frac{π}{6}$)图象上所有点向右平移$\frac{π}{6}$个单位得到函数y=g(x)的图象,则y=g(x)的图象的一条对称轴是直线( )| A. | x=$\frac{π}{12}$ | B. | x=$\frac{π}{6}$ | C. | x=-$\frac{π}{6}$ | D. | x=$\frac{2π}{3}$ |
分析 由条件利用y=Asin(ωx+φ)的图象变换规律求得g(x)的解析式,再利用正弦函数的图象的对称性,得出结论.
解答 解:将函数f(x)=sin(2x+$\frac{π}{6}$)图象上所有点向右平移$\frac{π}{6}$个单位得到函数y=g(x)=sin[2(x-$\frac{π}{6}$)+$\frac{π}{6}$]
=sin(2x-$\frac{π}{6}$)的图象,
令2x-$\frac{π}{6}$=kπ+$\frac{π}{2}$,求得x=$\frac{kπ}{2}$+$\frac{π}{3}$,k∈Z,
则y=g(x)的图象的一条对称轴是直线x=-$\frac{π}{6}$,
故选:C.
点评 本题主要考查y=Asin(ωx+φ)的图象变换规律,正弦函数的图象的对称性,属于基础题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
4.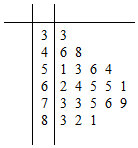 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
附:
(Ⅱ) 估计用户对该公司的产品“满意”的概率;
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到图3所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,(Ⅰ)根据以上资料完成下面的2×2列联表,若据此数据算得K2=3.7781,则在犯错的概率不超过5%的前提下,你是否认为“满意与否”与“性别”有关?
| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
(Ⅲ) 该公司为对客户做进一步的调查,从上述对其产品满意的用户中再随机选取2人,求这两人都是男用户或都是女用户的概率.
2.sin15°sin75°=( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{4}$ |
3.已知复数$z=\frac{2-i}{i^3}$(其中i是虚数单位,满足i2=-1),则z的共轭复数是( )
| A. | 1-2i | B. | 1+2i | C. | -1-2i | D. | -1+2i |
