题目内容
9.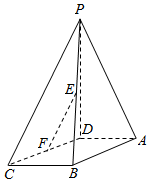 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.(1)求证:AB⊥面PAD;
(2)求证:EF∥面PAD.
分析 (1)经点D作DG∥AB,交BC于G点,可证四边形ABGD为平行四边形,利用勾股定理可证CG⊥DG,从而可证AB⊥AD,再证PD⊥AB,即可证明AB⊥平面PAD.
(2)取AB的中点M,连接FM,EM,可证EM∥PA,FM∥AD,既有面EFM∥面PAD,进而可证EF∥面PAD.
解答  证明:(1)经点D作DG∥AB,交BC于G点,
证明:(1)经点D作DG∥AB,交BC于G点,
∵AD∥BC,四边形ABGD为平行四边形,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,
∴CG=BC-BG=5,GD=AB=12,
∴CG2+GD2=52+122=CD2=132,
∴CG⊥DG,
∴AB⊥AD,
又∵PD⊥面ABCD,AB?面ABCD,
∴PD⊥AB,
∵PD∩AD=D,
∴AB⊥平面PAD
(2)取AB的中点M,连接FM,EM,
∵点E、F分别是棱PB、边CD的中点.
∴EM∥PA,FM∥AD,
∵EM∩FM=M,DA∩PA=A,
∴面EFM∥面PAD,
又∵EF?面EFM,
∴EF∥面PAD.
点评 本题主要考查了直线与平面垂直,直线与平面平行的判定,考查了空间想象能力和推理论证能力,属于中档题.

练习册系列答案
相关题目
20.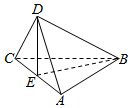 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
14.设全集U=R,集合A={x|x>0},B={x|x<1},则集合(∁UA)∩B=( )
| A. | (-∞,0) | B. | (-∞,0] | C. | (1,+∞) | D. | [1,+∞) |
1.幂函数y=f(x)的图象经过点(2,4),则f(x)的解析式为( )
| A. | f(x)=2x | B. | f(x)=x2 | C. | f(x)=2x | D. | f(x)=log2x+3 |
18.若m为实数且(2+mi)(m-2i)=-4-3i,则m=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |