题目内容
17.已知函数f(x)=sin2x+$\sqrt{3}sinxcosx,({x∈R})$.(1)求函数f(x)的最小正周期;
(2)当$x∈[{0,\frac{π}{2}}]$时,求f(x)的最大值和最小值.
分析 (1)由已知先求出f(x)=$sin({2x-\frac{π}{6}})+\frac{1}{2}$,由此能求出函数f(x)的最小正周期.
(2)由$x∈[{0,\frac{π}{2}}]$,得到$2x-\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],由此能求出f(x)的最大值和最小值.
解答 解:(1)f(x)=sin2x+$\sqrt{3}sinxcosx$
=$\frac{1-cos2x}{2}+\frac{\sqrt{3}}{2}sin2x$
=$\frac{\sqrt{3}}{2}sin2x-\frac{1}{2}cos2x+\frac{1}{2}$
=$sin({2x-\frac{π}{6}})+\frac{1}{2}$,…(6分)
函数f(x)的最小正周期为$\frac{2π}{2}=π$.…(8分)
(2)∵$x∈[{0,\frac{π}{2}}]$,∴$2x-\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],…(10分)
当$2x-\frac{π}{6}=-\frac{π}{6}即x=0$时,f(x)min=0,…(12分)
当$2x-\frac{π}{6}=\frac{π}{2}即x=\frac{π}{3}$时,$f{(x)_{max}}=\frac{3}{2}$.…(14分)
点评 本题考查函数的最小正周期的求法,考查函数的最小值和最大值的求法,是基础题,解题时要认真审题,注意三角函数性质的合理运用.

练习册系列答案
相关题目
12.短轴长等于8,离心率等于$\frac{3}{5}$的椭圆的标准方程为( )
| A. | $\frac{x^2}{100}+\frac{y^2}{64}=1$ | B. | $\frac{x^2}{100}+\frac{y^2}{64}=1$或$\frac{x^2}{64}+\frac{y^2}{100}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ |
7.已知函数f(x)是定义在R上的偶函数,若当x<0时,f(x)=-log2(-2x),则f(32)=( )
| A. | -32 | B. | -6 | C. | 6 | D. | 64 |
 如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.
如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.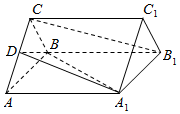 如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.
如图所示,正三棱柱ABC-A1B1C1的底面边长是2,侧棱长是$\sqrt{3}$,D是AC的中点.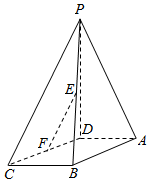 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.