题目内容
20.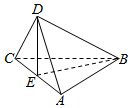 已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )
已知正方形ABCD的对角线AC与BD相交于E点,将△ACD沿对角线折起,使得平面ABC⊥平面ADC(如图),则下列命题中正确的是( )| A. | 直线AB⊥直线CD,且直线AC⊥直线BD | |
| B. | 直线AB⊥平面BCD,且直线AC⊥平面BDE | |
| C. | 平面ABC⊥平面BDE,且平面ACD⊥BDE | |
| D. | 平面ABD⊥平面BCD,且平面ACD⊥平面BDE |
分析 由直线AB⊥直线CD不成立,知A错误;由直线AB⊥平面BCD不成立,知B错误;由平面ABC⊥平面BDE,且平面ACD⊥平面BDE,知C正确;由平面ABD⊥平面BCD不成立,知D错误.
解答 解:由题意知DC⊥BE,AB∩BE=E,
∴直线AB⊥直线CD不成立,故A错误;
∵AC⊥AB,∴AB与BC不垂直,
∴直线AB⊥平面BCD不成立,故B错误;
∵BE⊥DE,BE⊥AC,∴AC⊥平面BDE,
∴平面ABC⊥平面BDE,且平面ACD⊥平面BDE,故C正确;
∵平面ABD⊥平面BCD不成立,故D错误.
故选:C.
点评 本题考查命题真假的判断,考查空间直线与直线、直线与平面、平面与平面的位置关系,是中档题.

练习册系列答案
相关题目
12.短轴长等于8,离心率等于$\frac{3}{5}$的椭圆的标准方程为( )
| A. | $\frac{x^2}{100}+\frac{y^2}{64}=1$ | B. | $\frac{x^2}{100}+\frac{y^2}{64}=1$或$\frac{x^2}{64}+\frac{y^2}{100}=1$ | ||
| C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{25}+\frac{y^2}{16}=1$或$\frac{x^2}{16}+\frac{y^2}{25}=1$ |
10.若复数z=$\frac{a+i}{2i}$(a∈R,i为虚数单位)的实部与虚部相等,则z的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
 如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.
如图,四棱锥P-ABCD中,∠BAD=∠ABC=90°,BC=2AD,△PAB和△PAD都是等边三角形,则异面直线CD与PB所成角的大小为90°.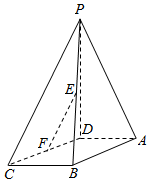 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.