题目内容
7.已知f(x)是定义在D上的函数,若f(x)满足:(1)对任意x∈D及任意正实数t,若x+t∈D,都有f(x+t)≥f(x);(2)存在正实数M,使得|f(x)|≤M,则称f(x)为“单限行函数”,满足|f(x)|≤M的最小正数M叫f(x)的“单限峰值”给出下列结论:①f(x)=2016(x∈[-1,2])是“单限行函数”;
②f(x)=xsinx+cosx(x∈[0,$\frac{π}{2}$])是“单限行函数”,且“单限峰值”为1;
③若f(x)=x3-12x(x∈[m,m+2])是“单限行函数”,则-4<m<2;
④f(x)是定义在D上的“单限行函数”,若f(x1)=f(x2),则x1=x2
其中正确结论的个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 根据“单限行函数”的定义分别判断函数的单调性和最值即可得到结论.
解答 解:①若f(x)=2016(x∈[-1,2]),
则f(x+t)=f(x)=2016,则f(x+t)≥f(x)恒成立;且|f(x)|=2016,且当M≥2016时,|f(x)|≤M成立,则f(x)是“单限行函数”;故①正确,
②f(x)=xsinx+cosx(x∈[0,$\frac{π}{2}$]),
则f′(x)=sinx+xcosx-sinx=xsinx≥0,则函数f(x)为增函数,
则f(x+t)≥f(x)恒成立,
f(0)=1,f($\frac{π}{2}$)=$\frac{π}{2}$,则|f(x)|≤$\frac{π}{2}$,即函数f(x)是“单限行函数”,且“单限峰值”为$\frac{π}{2}$,故②错误;
③f′(x)=3x2-12=3(x2-4),
由f′(x)>0得x>2或x<-2,由f′(x)<0得-2<x<2,
当m=2时,函数f(x)在[2,4]上增函数,满足f(x+t)≥f(x),
此时函数的最小值为f(2)=-16,最大值f(2)=16,则|f(x)|≤16,
m=2时,f(x)=x3-12x(x∈[2,4])是“单限行函数”,则-4<m<2错误;故③错误,
④f(x)是定义在D上的“单限行函数”,若f(x1)=f(x2),则x1=x2,不一定成立,比如①f(x)=2016(x∈[-1,2]),故④错误,
故选:A
点评 本题主要考查命题的真假判断,涉及函数的单调性和最值的判断,正确理解新定义是解决本题的关键.

练习册系列答案
相关题目
17.在某项测量中,测量结果X服从正态分布N(1,σ2)(σ>0),若X在(0,1)内取值的概率为0.4.则X在(0,2)内取值的概率为( )
| A. | 0.8 | B. | 0.6 | C. | 0.4 | D. | 0.2 |
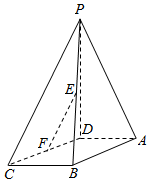 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.