题目内容
18.若m为实数且(2+mi)(m-2i)=-4-3i,则m=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 利用复数的运算法则、复数相等即可得出.
解答 解:∵(2+mi)(m-2i)=-4-3i,
∴4m+(m2-4)i=-4-3i,
∴$\left\{\begin{array}{l}{4m=-4}\\{{m}^{2}-4=-3}\end{array}\right.$,解得m=-1.
故选:A.
点评 本题考查了复数的运算法则、复数相等,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
3.已知复数z满足z(1+i)2=1-i,则复数z对应的点在( )上.
| A. | 直线y=-$\frac{1}{2}$x | B. | 直线y=$\frac{1}{2}$x | C. | 直线y=-$\frac{1}{2}$ | D. | 直线x=-$\frac{1}{2}$ |
10.若复数z=$\frac{a+i}{2i}$(a∈R,i为虚数单位)的实部与虚部相等,则z的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
7.已知函数f(x)是定义在R上的偶函数,若当x<0时,f(x)=-log2(-2x),则f(32)=( )
| A. | -32 | B. | -6 | C. | 6 | D. | 64 |
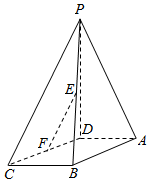 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.