题目内容
19.某家庭用分期付款的方式购买一辆汽车,价格为15万元,购买当天先付5万元,以后每月这一天都交付1万元,并加付欠款的利息,月利率为1%.若交付5万元以后的第一个月开始算分期付款的第一期,共10期付完,则全部货款付清后,买这辆汽车实际用的钱为15.55万元.分析 每月付1万元,分10次付完,设每月付款数顺次组成数列{an},可得付款数{an}组成等差数列,公差d=0,01,再利用等差数列的前n项和公式,求得结论.
解答 解:购买时付了5万元,欠款10万元.每月付1万元,分10次付完,设每月付款数顺次组成数列{an},
则a1=1+10×0.01=1.1,
a2=1+(10-1)×0.01=1.09,
a3=1+(10-2)×0.01=1.08,
a4=1+(10-3)×0.01=1.07
类推,得a10=1+(10-9)×0.01=1.01,
∴5+10+(0,01+0,02+…+0,1)=15.55;
故答案为:15.55.
点评 本题主要考查等差数列的实际应用,等差数列的前n项和公式,设每月付款数顺次组成数列{an},判断付款数{an}组成等差数列,公差d=-0.5,是解题的关键,属于中档题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
10.若复数z=$\frac{a+i}{2i}$(a∈R,i为虚数单位)的实部与虚部相等,则z的模等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
7.已知函数f(x)是定义在R上的偶函数,若当x<0时,f(x)=-log2(-2x),则f(32)=( )
| A. | -32 | B. | -6 | C. | 6 | D. | 64 |
11.在空间中,下列结论正确的是( )
| A. | 空间三点确定一个平面 | |
| B. | 过直线外一点有且只有一条直线与已知直线垂直 | |
| C. | 如果一条直线与平面内的一条直线平行,则这条直线与平面平行 | |
| D. | 三个平面最多将可空间分成八块 |
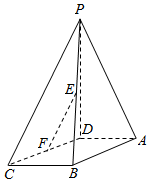 如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.
如图,在四棱锥P-ABCD中,PD⊥面ABCD,AD∥BC,CD=13,AB=12,BC=10,AD=$\frac{1}{2}$BC,点E、F分别是棱PB、边CD的中点.