题目内容
16.已知实数x,y满足约束条件$\left\{\begin{array}{l}x-y≥0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$,如果目标函数z=x+ay的最大值为$\frac{16}{3}$,则实数a的值为( )| A. | 3 | B. | $\frac{14}{3}$ | C. | 3或$\frac{14}{3}$ | D. | 3或$-\frac{11}{3}$ |
分析 由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,分类讨论代入目标函数求得a值.
解答 解:由约束条件$\left\{\begin{array}{l}x-y≥0\\ x+2y≤4\\ x-2y≤2\end{array}\right.$作出可行域如图,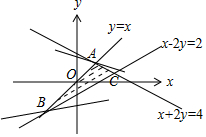
联立方程组分别解得:A($\frac{4}{3},\frac{4}{3}$),B(-2,-2),C(3,$\frac{1}{2}$).
化目标函数z=x+ay为y=$-\frac{x}{a}+\frac{z}{a}$.
当a>0时,由图可知,当直线y=$-\frac{x}{a}+\frac{z}{a}$过A或C时,直线在y轴上的截距最大,z有最大值为$\frac{16}{3}$.
若过A,则$\frac{16}{3}=\frac{4}{3}+\frac{4}{3}a$,解得a=3,符合题意;若过C,则$\frac{16}{3}=3+\frac{a}{2}$,解得a=$\frac{14}{3}$,不合题意;
当a<0时,由图可知,当直线y=$-\frac{x}{a}+\frac{z}{a}$过B或C时,直线在y轴上的截距最小,z有最大值为$\frac{16}{3}$.
若过B,则$\frac{16}{3}=-2-2a$,解得a=-$\frac{11}{3}$,符合题意;若过C,则$\frac{16}{3}=3+\frac{a}{2}$,解得a=$\frac{14}{3}$,不合题意.
∴a值为3或-$\frac{11}{3}$.
故选:D.
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案
相关题目
7.过抛物线y2=4x的焦点F且斜率为$2\sqrt{2}$的直线交抛物线于A,B两点(xA>xB),则$\frac{{|{AF}|}}{{|{BF}|}}$=( )
| A. | $\frac{3}{2}$ | B. | $\frac{3}{4}$ | C. | 3 | D. | 2 |
4.已知集合A={x|x2-2x-3<0},集合B={x|2x-1≥1},则A∩B=( )
| A. | [-1,3) | B. | [0,3) | C. | [1,3) | D. | (1,3) |
1.若同时掷两枚骰子,则向上的点数和是6的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{5}{18}$ |
6.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1、F2,其焦距为2c,点Q(c,$\frac{a}{2}$)在椭圆的内部,点P是椭圆C上的动点,且|PF1|+|PQ|<5|F1F2|恒成立,则椭圆离心率的取值范围是( )
| A. | ($\frac{1}{5}$,$\frac{\sqrt{2}}{2}$) | B. | ($\frac{1}{4}$,$\frac{\sqrt{2}}{2}$) | C. | ($\frac{1}{3}$,$\frac{\sqrt{2}}{2}$) | D. | ($\frac{2}{5}$,$\frac{\sqrt{2}}{2}$) |
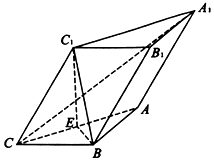 如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.
如图,在三棱柱ABC-A1B1C1中,平面A1ACC1⊥底面ABC,AB=BC=2,∠ACB=30°,∠C1CB=60°,BC1⊥A1C,E为AC的中点,侧棱CC1=2.