题目内容
函数f（x）=x2-2x+3在区间[1，m]上有最大值3，则m的值是 ．
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：求出函数f（x）的对称轴x=1，所以f（x）在[1，m]上单调递增，所以f（x）最大值为f（m）=3，这样即可求出m．
解答：
解：f（x）=x2-2x+3=（x-1）2+2；
∵f（x）在[1，m]上为增函数，∴最大值为（m-1）2+2=3，解得m=2或0（舍去）；
∴m的值是2．
故答案为：2．
∵f（x）在[1，m]上为增函数，∴最大值为（m-1）2+2=3，解得m=2或0（舍去）；
∴m的值是2．
故答案为：2．
点评：考查二次函数的对称轴及单调性，二次函数的最值．
练习册系列答案
相关题目
函数f（x）=-2x+ax3，若f′（2）=1，则a=（ ）
| A、4 | ||
B、
| ||
| C、-4 | ||
D、-
|
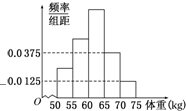如图是某学校抽取的学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1：2：3，第2小组的频数为10，则抽取的学生人数为（ ）数列{an}满足：a1a2a3…an=
，则a2013=（ ）
| 1 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|