题目内容
已知等差数列{an}的公差d≠0,a1≠d,若前20项的和S20=10M,则M等于( )
| A、a1+2a10 |
| B、a6+a15 |
| C、a20+d |
| D、2a10+2d |
考点:等差数列的前n项和
专题:等差数列与等比数列
分析:由等差数列的求和公式和性质易得M=a6+a15
解答:
解:由题意可得S20=
=10(a1+a20)=10M,
∴M=a1+a20,由等差数列的性质可得a1+a20=a6+a15,
∴M=a6+a15,
故选:B
| 20(a1+a20) |
| 2 |
∴M=a1+a20,由等差数列的性质可得a1+a20=a6+a15,
∴M=a6+a15,
故选:B
点评:本题考查等差数列的性质和求和公式,属基础题.

练习册系列答案
相关题目
在△ABC中,若-
sinAsinB<sin2A+sin2B-sin2C<-sinAsinB,则△ABC的形状是( )
| 3 |
| A、钝角三角形 | B、直角三角形 |
| C、锐角三角形 | D、不能确定 |
给出如图所示程序:执行该程序时,若输入x为4,则输出y值为( )


| A、3 | B、8 | C、9 | D、64 |
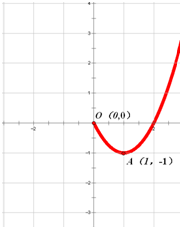 已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.
已知f(x)是定义在R上的奇函数,如图为函数f(x)的部分图象.