题目内容
在(
+
)6（a＞0）的展开式中含常数项的系数是60，则
sinxdx的值为 ．
| x |
| a |
| x |
| ∫ | a 0 |
考点：二项式系数的性质
专题：二项式定理
分析：利用二项展开式的通项公式求出通项，令x的指数为0，求出展开式的常数项，列出方程求出a，代入定积分求出值．
解答：
解：(
+
)6展开式的通项arC6rx
，令6-3r=0得r=2．
∴常数项为15a2=60，a=2，
∴
sinxdx=
sinxdx=（-cosx）
=1-cos2．
故答案为：1-cos2．
| x |
| a |
| x |
| 6-3r |
| 2 |
∴常数项为15a2=60，a=2，
∴
| ∫ | a 0 |
| ∫ | 2 0 |
| | | 2 0 |
故答案为：1-cos2．
点评：本题考查利用二项展开式的通项公式解决二项展开式的特定项问题、求定积分值．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
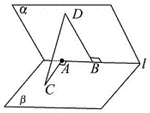如图，60°的二面角的棱上有A，B两点，直线AC，BD分别在这个二面角的两个半平面内，且都垂直于AB，已知AB=4，AC=6，BD=8，则CD的长为某算法的程序框图如图所示，若输入a=1，b=2，c=3，则输出的结果为（ ）
| A、1 | B、2 | C、3 | D、4 |