题目内容
长方体ABCD-A1B1C1D1中,AB=3,BC=2,AA1=1,一绳子从A沿着表面拉到C1的最短距离是( )
A、
| ||
B、2
| ||
C、3
| ||
D、
|
考点:多面体和旋转体表面上的最短距离问题
专题:操作型,空间位置关系与距离
分析:按三种不同方式展开长方体的侧面,计算平面图形中三条线段的长,比较得正确选项.
解答:
 解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为:
解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为:
=3
,
=2
,
=
.
三者比较得3
是从点A沿表面到C1的最短距离.
故选:C.
 解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为:
解:长方体ABCD-A1B1C1D1的表面可如图三种方法展开后,A、C1两点间的距离分别为:| (1+2)2+32 |
| 2 |
| (3+1)2+22 |
| 5 |
| (3+2)2+12 |
| 26 |
三者比较得3
| 2 |
故选:C.
点评:本题考查棱柱的结构特征,考查分类讨论思想,考查计算能力,属于中档题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
某算法的程序框图如图所示,若输入a=1,b=2,c=3,则输出的结果为( )


| A、1 | B、2 | C、3 | D、4 |
(理)已知数列{an}的通项公式an=n2-(6+2λ)n+2014,若a6或a7为数列{an}的最小项,则实数λ的取值范围( )
| A、(3,4) | ||||
| B、[2,5] | ||||
| C、[3,4] | ||||
D、[
|
若|
|=2|
|≠0,
⊥
,
=
+
,则
与
的夹角为( )
| b |
| a |
| c |
| a |
| c |
| a |
| b |
| a |
| b |
| A、30° | B、60° |
| C、90° | D、120° |
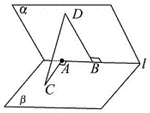 如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为
如图,60°的二面角的棱上有A,B两点,直线AC,BD分别在这个二面角的两个半平面内,且都垂直于AB,已知AB=4,AC=6,BD=8,则CD的长为