题目内容
3.若命题“?t∈R,t2-2t-a<0”是假命题,则实数a的取值范围是(-∞,-1].分析 命题“?t∈R,t2-2t-a<0”是假命题,则?t∈R,t2-2t-a≥0是真命题,可得△≤0.
解答 解:命题“?t∈R,t2-2t-a<0”是假命题,
则?t∈R,t2-2t-a≥0是真命题,
∴△=4+4a≤0,解得a≤-1.
∴实数a的取值范围是(-∞,-1].
故答案为:(-∞,-1].
点评 本题考查了方程与不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
18.已知函数f(x)=2f(2-x)-x2+5x-5,则曲线y=f(x)在点(1,f(1))处的切线方程为( )
| A. | y=x | B. | y=-2x+3 | C. | y=-3x+4 | D. | y=x-2 |
13.已知命题p:?x∈R,x2-mx+1=0,q:?x∈R,ex-m>0,若¬p∧q为真,则实数m的取值范围是( )
| A. | [-2,2] | B. | (-2,0] | C. | (-2,0) | D. | [0,2] |
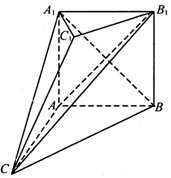 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,A1C=BC,B1C1∥BC,且${B_1}{C_1}=\frac{1}{2}BC$.