题目内容
如图,□ABCD中,∠ABC=75°,AF⊥BC于F,AF交BD于E,若DE=2AB,则∠AED的大小是( )


| A、60° | B、65° |
| C、70° | D、75° |
考点:解三角形
专题:计算题,解三角形
分析:由DE=2AB,可作辅助线:取DE中点O,连接AO,根据平行四边形的对边平行,易得△ADE是直角三角形,由直角三角形斜边上的中线是斜边的一半,即可得△ADO,△AOE,△AOB是等腰三角形,借助于方程求解即可.
解答:
 解:取DE中点O,连接AO,
解:取DE中点O,连接AO,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB=180°-∠ABC=105°,
∵AF⊥BC,
∴AF⊥AD,
∴∠DAE=90°,
∴OA=
DE=OD=OE,
∵DE=2AB,
∴OA=AB,
∴∠AOB=∠ABO,∠ADO=∠DAO,∠AED=∠EAO,
∵∠AOB=∠ADO+∠DAO=2∠ADO,
∴∠ABD=∠AOB=2∠ADO,
∴∠ABD+∠ADO+∠DAB=180°,
∴∠ADO=25°,∠AOB=50°,
∵∠AED+∠EAO+∠AOB=180°,
∴∠AED=65°.
故选:B.
 解:取DE中点O,连接AO,
解:取DE中点O,连接AO,∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAB=180°-∠ABC=105°,
∵AF⊥BC,
∴AF⊥AD,
∴∠DAE=90°,
∴OA=
| 1 |
| 2 |
∵DE=2AB,
∴OA=AB,
∴∠AOB=∠ABO,∠ADO=∠DAO,∠AED=∠EAO,
∵∠AOB=∠ADO+∠DAO=2∠ADO,
∴∠ABD=∠AOB=2∠ADO,
∴∠ABD+∠ADO+∠DAB=180°,
∴∠ADO=25°,∠AOB=50°,
∵∠AED+∠EAO+∠AOB=180°,
∴∠AED=65°.
故选:B.
点评:此题考查了直角三角形的性质(直角三角形斜边上的中线是斜边的一半)、平行四边形的性质(平行四边形的对边平行)以及等腰三角形的性质(等边对等角),解题的关键是注意方程思想的应用.

练习册系列答案
相关题目
下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是( )
| A、y=sinx |
| B、y=-x2 |
| C、y=lg2x |
| D、y=e|x| |
下列命题中:
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?x∈R,x2+2x≤0,则?p为:?x∈R,x2+2x>0.
③命题“若?p,则q”的逆否命题是“若p,则?q”.
其中正确结论的个数是( )
①若p,q为两个命题,则“p且q为真”是“p或q为真”的必要不充分条件.
②若p为:?x∈R,x2+2x≤0,则?p为:?x∈R,x2+2x>0.
③命题“若?p,则q”的逆否命题是“若p,则?q”.
其中正确结论的个数是( )
| A、1 | B、2 | C、3 | D、0 |
若cosα=-
,0<α<π,则tanα=( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设偶函数f(x)对任意x∈R,都有f(x+3)=-
,且当x∈[-3,-2]时,f(x)=4x,则f(1075)等于( )
| 1 |
| f(x) |
| A、8 | ||
B、
| ||
| C、-8 | ||
D、-
|
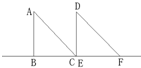 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


