题目内容
下列命题中正确的是( )
| A、由五个平面围成的多面体只能是四棱锥 |
| B、圆柱、圆锥、圆台的底面都是圆 |
| C、仅有一组对面平行的六面体是棱台 |
| D、有一个面是多边形,其余各面是三角形的几何体是棱锥 |
考点:棱锥的结构特征
专题:证明题,空间位置关系与距离
分析:对选项逐一验证,注意举反例.
解答:
解:选项A:由五个平面围成的多面体也可以是三棱柱;故不正确;
选项B:圆柱、圆锥、圆台的底面都是圆,正确;
选项C:仅有一组对面平行的六面体也可以是四棱柱,故不正确;
选项D:有一个面是多边形,其余各面是三角形的几何体也可以是八面体,故不正确.
故选B.
选项B:圆柱、圆锥、圆台的底面都是圆,正确;
选项C:仅有一组对面平行的六面体也可以是四棱柱,故不正确;
选项D:有一个面是多边形,其余各面是三角形的几何体也可以是八面体,故不正确.
故选B.
点评:考查了学生的空间想象力;注意举反例.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
设偶函数f(x)对任意x∈R,都有f(x+3)=-
,且当x∈[-3,-2]时,f(x)=4x,则f(1075)等于( )
| 1 |
| f(x) |
| A、8 | ||
B、
| ||
| C、-8 | ||
D、-
|
圆x2+y2-2x-2y=0上的点到直线x+y+2=0的距离最大为( )
A、
| ||
B、2
| ||
C、3
| ||
D、2+2
|
定义在R上的可导函数f(x)的导函数为f′(x),满足f′(x)>f(x),f(0)=1,则不等式f(x)<ex的解集为( )
| A、(-∞,6) |
| B、(6,+∞) |
| C、(0,+∞) |
| D、(-∞,0) |
图为一个半球挖去一个圆锥的几何体的三视图,则该几何体的体积为( )


A、
| ||
| B、8π | ||
C、
| ||
D、
|
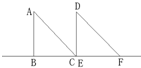 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


