题目内容
设Sn为等比数列{an}的前n项和,已知3S3=a4-2,3S2=a3-2,则公比q=( )
| A、3 | B、4 | C、5 | D、6 |
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:3S3=a4-2,3S2=a3-2,两式相减得3a3=a4-a3,由此能求出公比q=4.
解答:
解:∵Sn为等比数列{an}的前n项和,3S3=a4-2,3S2=a3-2,
两式相减得
3a3=a4-a3,
a4=4a3,
∴公比q=4.
故选:B.
两式相减得
3a3=a4-a3,
a4=4a3,
∴公比q=4.
故选:B.
点评:本题考查公比的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
若cosα=-
,0<α<π,则tanα=( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
设函数f(x)=x2-1,若f(a)=3,则实数a的值为( )
| A、2 | B、4 | C、-2 | D、2或-2 |
下列命题为真命题的是( )
| A、若p∨q为真命题,则p∧q为真命题 |
| B、“x=5”是“x2-4x-5=0”的充分不必要条件 |
| C、命题“若x<-1,则x2-2x-3>0”的否命题为“若x<-1,则x2-2x-3≤0” |
| D、已知命题p:?x∈R,使得x2+x-1<0,¬p:?x∈R,使得x2+x-1>0 |
不等式ax2+ax-3<0解集为R,则a的取值范围是( )
| A、-12≤a<0 |
| B、a>-12 |
| C、-12<a≤0 |
| D、a<0 |
设偶函数f(x)对任意x∈R,都有f(x+3)=-
,且当x∈[-3,-2]时,f(x)=4x,则f(1075)等于( )
| 1 |
| f(x) |
| A、8 | ||
B、
| ||
| C、-8 | ||
D、-
|
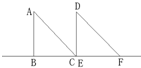 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


