题目内容
对于命题p和q,若p且q为真命题,则下列四个命题:
①p或¬q是真命题;
②p且¬q是真命题;
③¬p且¬q是假命题;
④¬p或q是假命题.
其中真命题是( )
①p或¬q是真命题;
②p且¬q是真命题;
③¬p且¬q是假命题;
④¬p或q是假命题.
其中真命题是( )
| A、①② | B、③④ | C、①③ | D、②④ |
考点:复合命题的真假
专题:简易逻辑
分析:先判断命题p,q的真假,然后判断¬p,¬q的真假,并判断由逻辑连接词“或“,“且“,连接的复合命题的真假.
解答:
解:∵p且q为真命题;
∴p,q都为真命题;
①p或¬q是真命题,正确,∵p和¬q中,p是真命题;
②p且¬q是真命题,错误,∵p和¬q中,¬q是假命题,∴p且¬q是假命题;
③¬p且¬q是假命题,正确,∵¬p和¬q都为假命题;
④¬p或q是假命题,错误,∵¬p和q中q是真命题,∴¬p或q是真命题.
∴其中真命题是:①③.
故选:C.
∴p,q都为真命题;
①p或¬q是真命题,正确,∵p和¬q中,p是真命题;
②p且¬q是真命题,错误,∵p和¬q中,¬q是假命题,∴p且¬q是假命题;
③¬p且¬q是假命题,正确,∵¬p和¬q都为假命题;
④¬p或q是假命题,错误,∵¬p和q中q是真命题,∴¬p或q是真命题.
∴其中真命题是:①③.
故选:C.
点评:考查由“且“,“或“连接的复合命题p且q,p或q的真假和命题p,q真假的关系,p和¬p真假的关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列命题为真命题的是( )
| A、若p∨q为真命题,则p∧q为真命题 |
| B、“x=5”是“x2-4x-5=0”的充分不必要条件 |
| C、命题“若x<-1,则x2-2x-3>0”的否命题为“若x<-1,则x2-2x-3≤0” |
| D、已知命题p:?x∈R,使得x2+x-1<0,¬p:?x∈R,使得x2+x-1>0 |
不等式ax2+ax-3<0解集为R,则a的取值范围是( )
| A、-12≤a<0 |
| B、a>-12 |
| C、-12<a≤0 |
| D、a<0 |
已知f(x)=
,若f(0)是f(x)的最小值,则t的取值范围为( )
|
| A、[-1,2] |
| B、[-1,0] |
| C、[1,2] |
| D、[0,2] |
设偶函数f(x)对任意x∈R,都有f(x+3)=-
,且当x∈[-3,-2]时,f(x)=4x,则f(1075)等于( )
| 1 |
| f(x) |
| A、8 | ||
B、
| ||
| C、-8 | ||
D、-
|
圆x2+y2-2x-2y=0上的点到直线x+y+2=0的距离最大为( )
A、
| ||
B、2
| ||
C、3
| ||
D、2+2
|
图为一个半球挖去一个圆锥的几何体的三视图,则该几何体的体积为( )


A、
| ||
| B、8π | ||
C、
| ||
D、
|
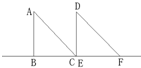 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


