题目内容
设全集U=R,A={x|x2+3x<0},B={x|x<-1},则图中阴影部分表示的集合为( )


| A、{x|-1<x<0} |
| B、{x|-1≤x<0} |
| C、{x|0<x<3} |
| D、{x|-3<x≤-1} |
考点:Venn图表达集合的关系及运算
专题:集合
分析:根据Venn图,得到集合关系为A∩(∁UB),然后根据集合的基本运算求解即可.
解答:
解:由Venn图,得到阴影部分对应的集合为A∩(∁UB),
∵A={x|x2+3x<0}={x|-3<x<0},B={x|x<-1},
∴(∁UB)={x|x≥-1},
∴A∩(∁UB)={x|-1≤x<0},
故选:B
∵A={x|x2+3x<0}={x|-3<x<0},B={x|x<-1},
∴(∁UB)={x|x≥-1},
∴A∩(∁UB)={x|-1≤x<0},
故选:B
点评:本题主要考查集合的基本运算,利用Venn图确定集合关系是解决本题的关键,比较基础.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列函数中既是奇函数,又在区间(0,+∞)上单调递增的是( )
| A、y=sinx |
| B、y=-x2 |
| C、y=lg2x |
| D、y=e|x| |
若cosα=-
,0<α<π,则tanα=( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
已知角α的终边经过点P(-4a,3a),(a≠0)则2sinα+cosα=( )
| A、-0.4 | B、0.4 |
| C、0 | D、±0.4 |
设函数f(x)=x2-1,若f(a)=3,则实数a的值为( )
| A、2 | B、4 | C、-2 | D、2或-2 |
不等式ax2+ax-3<0解集为R,则a的取值范围是( )
| A、-12≤a<0 |
| B、a>-12 |
| C、-12<a≤0 |
| D、a<0 |
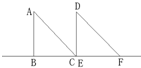 如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )
如图,△ABC和△DEF是两个形状大小完全相同的等腰直角三角形,∠B=∠DEF=90°,点B、C、E、F在同一直线上.现从点C、E重合的位置出发,让△ABC在直线EF上向右作匀速运动,而△DEF的位置不动.设两个三角形重合部分的面积为y,运动的距离为x.下面表示y与x的函数关系式的图象大致是( )


