题目内容
集合A={x|-2≤x≤5},集合B={x|m+1≤x≤2m-1}.
(1)若B⊆A,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
(1)若B⊆A,求实数m的取值范围;
(2)当x∈R时,没有元素x使x∈A与x∈B同时成立,求实数m的取值范围.
考点:元素与集合关系的判断
专题:集合
分析:(1)根据B⊆A讨论B=∅和B≠∅两种情况,B=∅时容易求得m<2,B≠∅时,m需满足
,解该不等式组求出m的范围,然后并上m<2即得实数m的取值范围;
(2)由题意知:A∩B=∅,B=∅时,由(1)求得m<2.B≠∅时,m需满足
,解该不等式组,所得解并上m<2即可.
|
(2)由题意知:A∩B=∅,B=∅时,由(1)求得m<2.B≠∅时,m需满足
|
解答:
解:(1)若B⊆A,B=∅时,m+1>2m-1,∴m<2,满足B⊆A;
B≠∅时,则
,解得2≤m≤3;
综上所述,当m≤3时有B⊆A;
即实数m的取值范围为(-∞,3];
(2)由题意知,A∩B=∅;
∴B=∅时,m+1>2m-1,∴m<2;
B≠∅时,则
,解得:m>4;
∴实数m的取值范围为(-∞∞,2)∪(4,+∞).
B≠∅时,则
|
综上所述,当m≤3时有B⊆A;
即实数m的取值范围为(-∞,3];
(2)由题意知,A∩B=∅;
∴B=∅时,m+1>2m-1,∴m<2;
B≠∅时,则
|
∴实数m的取值范围为(-∞∞,2)∪(4,+∞).
点评:考查子集的概念,空集的概念,以及交集的概念,不要漏了B=∅的情况.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知函数f(2x-1)的定义域为(1,2),则函数f(x+1)的定义域为( )
| A、(0,2) |
| B、(1,2) |
| C、(1,3) |
| D、(0,3) |
若定义在R上的函数f(x)的导函数为f'(x),且满足f'(x)>f(x),则f(2011)与f(2009)e2的大小关系为( )
| A、f(2011)<f(2009)e2 |
| B、f(2011)=f(2009)e2 |
| C、f(2011)>f(2009)e2 |
| D、不能确定 |
若变量x、y满足
,若2x-y的最大值为-1,则a=( )
|
| A、-1 | B、1 | C、-2 | D、2 |
某个几何体的三视图如图(其中正视图中的圆弧是半圆)所示,则该几何体的表面积为( )
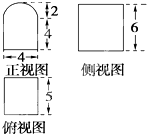

| A、92+24π |
| B、82+14π |
| C、92+14π |
| D、82+24π |
设公差d≠0的等差数列{an}中,a1,a3,a9成等比数列,则
=( )
| a1+a3+a5 |
| a2+a4+a6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
若x<
,则
等于( )
| 1 |
| 3 |
| 1-6x+9x2 |
| A、3x-1 |
| B、1-3x |
| C、(1-3x)2 |
| D、非以上答案 |