题目内容
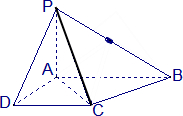 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=| 1 |
| 2 |
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角的余弦值;
(Ⅲ)求线BP与面PAC所成角的余弦值.
考点:直线与平面所成的角,异面直线及其所成的角,平面与平面垂直的判定
专题:空间位置关系与距离,空间角,空间向量及应用
分析:利用向量法求解:
以点A为坐标原点,射线AD为x轴正半轴,射线AB为y轴正半轴,射线AP为z轴正半轴建立空间直角坐标系.
对于第(1)问,求出平面PAD的一个法向量和平面PCD的一个法向量,要证明两平面垂直,只需说明这两个法向量互相垂直即可;
对于第(2)问,由cos<
,
>=
,可探求AC与PB所成的角的余弦值;
对于第(3)问,先求出平面PAC的一个法向量,再求得此法向量与向量
所成角的余弦值,根据此余弦值与直线BP与面PAC所成角的余弦值的关系可达到目的.
以点A为坐标原点,射线AD为x轴正半轴,射线AB为y轴正半轴,射线AP为z轴正半轴建立空间直角坐标系.
对于第(1)问,求出平面PAD的一个法向量和平面PCD的一个法向量,要证明两平面垂直,只需说明这两个法向量互相垂直即可;
对于第(2)问,由cos<
| AC |
| BP |
| ||||
|
|
对于第(3)问,先求出平面PAC的一个法向量,再求得此法向量与向量
| BP |
解答:
解:如右图所示,以点A为坐标原点,射线AD为x轴正半轴,射线AB为y轴正半轴,射线AP为z轴正半轴建立空间直角坐标系.
由题中条件得A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),
=(0,0,1),
=(0,2,0),
=(0,1,0),
=(-1,0,1),
=(1,1,0),
=(0,-2,1).
(Ⅰ)证明:设向量
=(x1,y1,z1)是平面PDC的法向量,
则由
,得
,即
,
取x1=1,得
=(1,0,1),显然向量
是平面PAD的一个法向量,
由
•
=0,知
⊥
,从而平面PAD⊥平面PCD,得证.
(Ⅱ)则cos<
,
>=
=
=-
,又异面直线AC与PB所成角的范围是(0,
],
所以直线AC与PB所成角的余弦值为
.
(Ⅲ)设向量
=(x2,y2,z2)是平面PAC的法向量,则
,
即
,得
,
取x2=1,则
=(1,-1,0),从而cos<
,
>=
=
=
.
设直线BP与平面PAC所成角为θ,则sinθ=
,从而cosθ=
=
,即直线BP与平面PAC所成角的余弦值为
.
由题中条件得A(0,0,0),B(0,2,0),C(1,1,0),D(1,0,0),P(0,0,1),
| AP |
| AB |
| DC |
| DP |
| AC |
| BP |

(Ⅰ)证明:设向量
| n1 |
则由
|
|
|
取x1=1,得
| n1 |
| AB |
由
| n1 |
| AB |
| n1 |
| AB |
(Ⅱ)则cos<
| AC |
| BP |
| ||||
|
|
| -2 | ||||
|
| ||
| 5 |
| π |
| 2 |
所以直线AC与PB所成角的余弦值为
| ||
| 5 |
(Ⅲ)设向量
| n2 |
|
即
|
|
取x2=1,则
| n2 |
| n2 |
| BP |
| ||||
|
|
| 2 | ||||
|
| ||
|
设直线BP与平面PAC所成角为θ,则sinθ=
| ||
|
| ||
|
| ||
| 5 |
| ||
| 5 |
点评:本题考查了两平面垂直的判定方法,两异面直线所成角的求法及线面角的求法,求解时应注意以下几点:
(1)首先应根据几何体的特点,选择三个两两垂直的方向,建立空间直角坐标系,标出所需的点及向量的坐标,再利用夹角公式进行计算,注意弄清由夹角公式得到的角与所求角的关系;
(2)找平面的法向量是关键,有时可直接观察出平面的法向量,这样可省去一些计算;
(3)坐标法是将严密的逻辑推理转化为坐标运算,一般很少添加其他辅助线,但有时计算繁琐,且易出错.
(1)首先应根据几何体的特点,选择三个两两垂直的方向,建立空间直角坐标系,标出所需的点及向量的坐标,再利用夹角公式进行计算,注意弄清由夹角公式得到的角与所求角的关系;
(2)找平面的法向量是关键,有时可直接观察出平面的法向量,这样可省去一些计算;
(3)坐标法是将严密的逻辑推理转化为坐标运算,一般很少添加其他辅助线,但有时计算繁琐,且易出错.

练习册系列答案
相关题目
已知函数f(x)=x2-2(a+2)x+a2,g(x)=-x2+2(a-2)x-a2+8.设 H1(X)=max{f(x),g(x)},max{p,q}表示p,q中的较大值,min{p,q}表示p,q中的较小值,记H1(x)的最小值为A,H2(x)的最大值为B,则A-B=( )
| A、a2-2a-16 |
| B、a2+2a-16 |
| C、16 |
| D、-16 |
已知集合A={x∈N|1<x<5},集合B={x∈N|2<x<6},则A∩B=( )
| A、{2,3} |
| B、{4,3} |
| C、{5,3} |
| D、{44,5} |
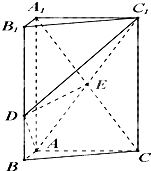 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=