题目内容
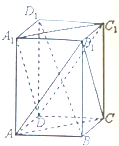 如图,在长方体ABCD-A1B1C1D1中,BB1=BC.
如图,在长方体ABCD-A1B1C1D1中,BB1=BC.(1)求证:平面DA1C1∥平面B1AC;
(2)求证:B1C⊥BD1.
考点:平面与平面平行的判定
专题:空间位置关系与距离
分析:(1)充分利用已知长方体的性质,结合面面平行的判定定理,只要判断DA1∥平面B1AC和A1C1∥平面B1AC即可;
(2)只要证明B1C⊥平面BC1D1,利用线面垂直的性质得到所证.
(2)只要证明B1C⊥平面BC1D1,利用线面垂直的性质得到所证.
解答:
证明:(1)∵四边形A1B1CD为平行四边形,∴DA1∥CB1…(1分)
∵CB1?平面B1AC,DA1?平面B1AC,∴DA1∥平面B1AC…(2分)
∵四边形A1C1CA为平行四边形,∴A1C1∥CA…(3分)
∵CA?平面B1AC,A1C1?平面B1AC∴A1C1∥平面B1AC…(4分)
∵DA1,A1C1是平面DA1C1内的两条相交直线 …(5分)
∴平面DA1C1∥平面B1AC…(6分)
(2)连接BC1,∵BB1=BC,∴在正方形BCC1B1中,B1C⊥BC1…(7分)
∵D1C1⊥平面BCC1B1∴B1C⊥D1C1…(9分)
∵BC1,D1C1是平面BC1D1内的两条相交直线
∴B1C⊥平面BC1D1…(11分)
∵BD1?平面BC1D1
∴B1C⊥BD1…(12分)
∵CB1?平面B1AC,DA1?平面B1AC,∴DA1∥平面B1AC…(2分)
∵四边形A1C1CA为平行四边形,∴A1C1∥CA…(3分)
∵CA?平面B1AC,A1C1?平面B1AC∴A1C1∥平面B1AC…(4分)
∵DA1,A1C1是平面DA1C1内的两条相交直线 …(5分)
∴平面DA1C1∥平面B1AC…(6分)
(2)连接BC1,∵BB1=BC,∴在正方形BCC1B1中,B1C⊥BC1…(7分)
∵D1C1⊥平面BCC1B1∴B1C⊥D1C1…(9分)
∵BC1,D1C1是平面BC1D1内的两条相交直线
∴B1C⊥平面BC1D1…(11分)
∵BD1?平面BC1D1
∴B1C⊥BD1…(12分)
点评:本题考查了长方体中面面平行的判定和线线垂直的判定,关键是准确利用长方体的性质结合面面平行的判定定理解答,属于基础题.

练习册系列答案
相关题目
设A是棱长为a的正方体的一个顶点,过从此顶点出发的三条棱的中点作截面,对正方体的所有顶点都如此操作,所得的各截面与正方体各面共同围成一个多面体,则关于此多面体有以下结论:
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
a3.
其中正确的结论是( )
①有12个顶点;②有24条棱;③有12个面;④表面积为3a2;⑤体积为
| 5 |
| 6 |
其中正确的结论是( )
| A、①③④ | B、①②⑤ |
| C、②③⑤ | D、②④⑤ |
如图所示,甲、乙、丙是三个空间立体图形的三视图,甲、乙、丙对应的标号正确的是( )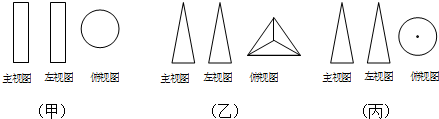
①长方体 ②圆锥 ③三棱锥 ④圆柱.

①长方体 ②圆锥 ③三棱锥 ④圆柱.
| A、③②④ | B、②①③ |
| C、①②③ | D、④③② |
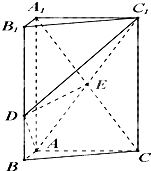 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
 对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所
对某同学的6次数学测试成绩(满分100分)进行统计,作出的茎叶图如图所