题目内容
已知α为锐角,且tanα=
-1,函数f(x)=2xtan2α+sin(2α+
),数列{an}的首项a1=1,an+1=f(an).
(1)求函数f(x)的表达式;
(2)若数列{bn}满足b1=a1,bn=log2(an+1),设Tn=
+
+…+
,若Tn>m对n≥2恒成立,求实数m的取值范围.
| 2 |
| π |
| 4 |
(1)求函数f(x)的表达式;
(2)若数列{bn}满足b1=a1,bn=log2(an+1),设Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
考点:数列与三角函数的综合
专题:计算题,等差数列与等比数列,三角函数的求值
分析:(1)由α为锐角,且tanα=
-1可求得tan2α=1,2α=
,sin(2α+
)=1,从而求出函数f(x)的表达式;
(2)由(1)知,an+1=f(an)=2an+1可推出an+1+1=2(an+1),又由a1=1,则数列{an+1}是以2为首项,2为公比的等比数列,从而求出an+1=2n,进而可得bn=log2(an+1)=log22n=n,代入可得Tn=
+
+…+
=
+
+
+…+
,可证明Tn+1-Tn=
+
-
>0,从而求若Tn>m对n≥2恒成立化为T2>m,从而求解.
| 2 |
| π |
| 4 |
| π |
| 4 |
(2)由(1)知,an+1=f(an)=2an+1可推出an+1+1=2(an+1),又由a1=1,则数列{an+1}是以2为首项,2为公比的等比数列,从而求出an+1=2n,进而可得bn=log2(an+1)=log22n=n,代入可得Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
| 1 |
| 1+n |
| 1 |
| 2+n |
| 1 |
| 3+n |
| 1 |
| 2n |
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
解答:
解:(1)∵tanα=
-1,
∴tan2α=
=1,
又∵α为锐角,
∴2α=
,
∴sin(2α+
)=sin
=1,
∴f(x)=2x+1;
(2)∵a1=1,an+1=f(an)=2an+1,
∴an+1+1=2(an+1),
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
则b1=1,bn=log2(an+1)=log22n=n,
则Tn=
+
+…+
=
+
+
+…+
,
Tn+1-Tn=
+
-
>0,
则对n≥2,当n=2时,Tn取得最小值,
T2=
+
=
,
则m<
.
| 2 |
∴tan2α=
2(
| ||
1-(
|
又∵α为锐角,
∴2α=
| π |
| 4 |
∴sin(2α+
| π |
| 4 |
| π |
| 2 |
∴f(x)=2x+1;
(2)∵a1=1,an+1=f(an)=2an+1,
∴an+1+1=2(an+1),
∴数列{an+1}是以2为首项,2为公比的等比数列,
∴an+1=2n,
则b1=1,bn=log2(an+1)=log22n=n,
则Tn=
| 1 |
| b1+n |
| 1 |
| b2+n |
| 1 |
| bn+n |
| 1 |
| 1+n |
| 1 |
| 2+n |
| 1 |
| 3+n |
| 1 |
| 2n |
Tn+1-Tn=
| 1 |
| 2n+1 |
| 1 |
| 2n+2 |
| 1 |
| n+1 |
则对n≥2,当n=2时,Tn取得最小值,
T2=
| 1 |
| 1+2 |
| 1 |
| 2+2 |
| 7 |
| 12 |
则m<
| 7 |
| 12 |
点评:本题考查了三角恒变换及等差等比数列的求法,用到了二倍角公式,构造数列及递增数列的判断,属于中档题.

练习册系列答案
相关题目
已知集合A={x∈N|1<x<5},集合B={x∈N|2<x<6},则A∩B=( )
| A、{2,3} |
| B、{4,3} |
| C、{5,3} |
| D、{44,5} |
设M(x0,y0)为抛物线C:y=
x2上一点,F为抛物线C的焦点,以F为圆心、|FM|为半径的圆和抛物线C的准线相交,则y0的取值范围是( )
| 1 |
| 8 |
| A、(2,+∞) | ||
| B、[0,2] | ||
C、(0,
| ||
D、(
|
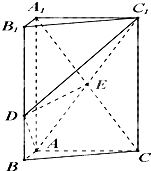 如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=
如图,三棱柱ABC-A1B1C1中,AA1⊥平面ABC,∠BAC=90°,AB=2,AC=6,点D在线段BB1上,且BD=