题目内容
6.设函数f(x)=$\left\{\begin{array}{l}{log_3}x,0<x≤9\\ f(x-4),x>9\end{array}$则$f(13)+2f(\frac{1}{3})$的值为( )| A. | 1 | B. | 0 | C. | -2 | D. | 2 |
分析 由已知先求出f(13)=f(9)=log39=2,f($\frac{1}{3}$)=log3$\frac{1}{3}$=-1,由此能求出$f(13)+2f(\frac{1}{3})$.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{log_3}x,0<x≤9\\ f(x-4),x>9\end{array}$,
∴f(13)=f(9)=log39=2,
f($\frac{1}{3}$)=log3$\frac{1}{3}$=-1,
$f(13)+2f(\frac{1}{3})$=2+2(-1)=0.
故选:B.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
16.设f(x)为定义在R上的奇函数,当x≥0时,f(x)=2x+2x+b,则b为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 无法确定 |
14.已知正项数列{an}的前n项和为Sn,当n≥2时,(an-Sn-1)2=SnSn-1,且a1=1,设bn=log2$\frac{{a}_{n+1}}{6}$,则bn等于( )
| A. | 2n-3 | B. | 2n-4 | C. | n-3 | D. | n-4 |
11.已知数列{an}中,a1=1,a2=3,an+2+an=an+1,则a2014=( )
| A. | -3 | B. | -1 | C. | 2 | D. | 3 |
15.如果$a+\frac{1}{a}=2$,那么${a^2}+\frac{1}{a^2}$的值是( )
| A. | 2 | B. | 4 | C. | 0 | D. | -4 |
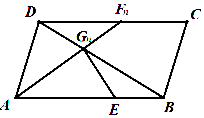 如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( )
如图,已知点E为平行四边形ABCD的边AB上一点,$\overrightarrow{AE}$=2$\overrightarrow{EB}$,Fn(n∈N*)为边DC上的一列点,连接AFn交BD于Gn,点Gn(n∈N*)满足$\overrightarrow{{G_n}D}$=$\frac{1}{3}$an+1$\overrightarrow{{G_n}A}$-(3an+2)$\overrightarrow{{G_n}E}$,其中数列{an}是首项为1的正项数列,则a4的值为( ) 甲、乙两名同学在五次考试中的数学成绩统计用茎叶图表示如图所示,则甲、乙两名同学成绩稳定的是乙.
甲、乙两名同学在五次考试中的数学成绩统计用茎叶图表示如图所示,则甲、乙两名同学成绩稳定的是乙.