题目内容
已知a＞0，b＞0，c＞0，求证：
（1）（
+
+
）（
+
+
）≥9；
（2）（a+b+c）（a2+b2+c2）≥9abc．
（1）（
| a |
| b |
| b |
| c |
| c |
| a |
| b |
| a |
| c |
| b |
| a |
| c |
（2）（a+b+c）（a2+b2+c2）≥9abc．
考点：不等式的证明
专题：选作题,不等式
分析：（1）利用柯西不等式，即可得出结论；
（2）利用基本不等式，即可证明结论．
（2）利用基本不等式，即可证明结论．
解答：
证明：（1）∵(
×
+
×
+
×
)2=(1×1+1×1+1×1)2，
又由柯西不等式得，(
×
+
×
+
×
)2=(1×1+1×1+1×1)2≤[（
）2+（
）2+（
）2][（
）2+（
）2+（
）2]
∴有(
+
+
)(
+
+
)≥9
（2）∵a+b+c≥3
，又∵a2+b2+c2≥3
∴（a+b+c）（a2+b2+c2）≥9abc
|
|
|
|
|
|
又由柯西不等式得，(
|
|
|
|
|
|
|
|
|
|
|
|
∴有(
| a |
| b |
| b |
| c |
| c |
| a |
| b |
| a |
| c |
| b |
| a |
| c |
（2）∵a+b+c≥3
| 3 | abc |
| 3 | a2b2c2 |
∴（a+b+c）（a2+b2+c2）≥9abc
点评：本题考查不等式的证明，正确运用不等式的证明方法是关键．
练习册系列答案
相关题目
已知数列{an}中，a3=2，a5=1，若{
}是等差数列，则a11等于（ ）
| 1 |
| 1+an |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
已知点A（1，0）、B（2，0），点C在y轴的正半轴上，求∠ACB取最大值时，C点的坐标．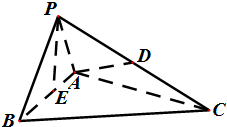
如图，四面体P-ABC中，△PAB为边长为1的等边三角形，△PBC与△PAC均为斜边为PC的直角三角形，且PC=