题目内容
设集合M={y|y=|sinx|，x∈R}，N={x||x|＜1}，则M∩N=（ ）
| A、（0，1） |
| B、（0，1] |
| C、[0，1） |
| D、[0，1] |
考点：交集及其运算
专题：集合
分析：由正弦函数的性质求出集合M，由|x|＜1求出集合N，由交集的运算求出M∩N．
解答：
解：由y=|sinx|得，0≤y≤1，则集合M=[0，1]，
由|x|＜1得，-1＜x＜1，则集合N=（-1，1），
所以M∩N=[0，1），
故选：C．
由|x|＜1得，-1＜x＜1，则集合N=（-1，1），
所以M∩N=[0，1），
故选：C．
点评：本题考查了交集及其运算，以及正弦函数的性质，属于基础题．
练习册系列答案
口算小状元口算速算天天练系列答案
相关题目
已知f（x）为R上的增函数，且f（log2x）＞f（1），则x的取值范围为（ ）
| A、（2，+∞） | ||
B、（0，
| ||
C、（
| ||
| D、（0，1）∪（2，+∞） |
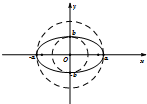圆锥曲线中不同曲线的性质都是有一定联系的，比如圆可以看成特殊的椭圆，所以很多圆的性质结论可以类比到椭圆，例如；如图所示，椭圆C：函数f（x）=
+lg（3x+1）的定义域为（ ）
| x2+4 | ||
|
A、（-
| ||||
B、（-∞，-
| ||||
C、（-
| ||||
D、（-
|