题目内容
18.已知集合A={y|y=log2x,x>1},B={x|y=$\frac{1}{\sqrt{1-2x}}$},则A∩B=( )| A. | {y|0<y<$\frac{1}{2}$} | B. | {y|0<y<1} | C. | {y|$\frac{1}{2}$<y<1} | D. | ∅ |
分析 求出集合的等价条件,结合交集运算进行求解即可.
解答 解:A={y|y=log2x,x>1}={y|y>0},
B={x|y=$\frac{1}{\sqrt{1-2x}}$}={x|1-2x>0}={x|x<$\frac{1}{2}$},
则A∩B={y|0<y<$\frac{1}{2}$},
故选:A
点评 本题主要考查集合的基本运算,求出集合的等价条件是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.在平面直角坐标系内,区域M满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤1\end{array}$区域N满足$\left\{\begin{array}{l}0≤x≤π\\ 0≤y≤sinx\end{array}$则向区域M内投一点,落在区域N内的概率是( )
| A. | $\frac{2}{π}$ | B. | $\frac{π}{4}$ | C. | 2-$\frac{2}{π}$ | D. | 2-$\frac{π}{4}$ |
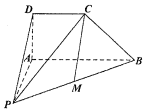 如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.
如图,在四棱锥P-ABCD中,CD∥AB,AD=DC=$\frac{1}{2}$AB.