题目内容
6.已知a,b,c分别为△ABC三个内角A,B,C所对的边长,且acosB-bcosA=$\frac{3}{5}$c.(Ⅰ)求$\frac{tanA}{tanB}$的值;
(Ⅱ)若A=60°,求$\frac{absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$的值.
分析 (Ⅰ)△ABC中,由条件利用正弦定理可得sinAcosB-sinBcosA=$\frac{3}{5}$sinC.又sinC=sin(A+B)=sinAcosB+cosAsinB,可得$\frac{2}{5}$sinAcosB=$\frac{8}{5}$sinBcosA,由此可得$\frac{tanA}{tanB}$的值.
(Ⅱ)可求tanA=$\sqrt{3}$,由(Ⅰ)得tanB=$\frac{\sqrt{3}}{4}$.利用余弦定理,两角和的正切函数公式即可化简求值.
解答 解:(1)△ABC中,由条件利用正弦定理$\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}$,
可得sinAcosB-sinBcosA=$\frac{3}{5}$sinC.(2分)
又sinC=sin(A+B)=sinAcosB+cosAsinB,所以,$\frac{2}{5}$sinAcosB=$\frac{8}{5}$sinBcosA,(5分)
可得$\frac{tanA}{tanB}$=$\frac{sinAcosB}{sinBcosA}=4$.(7分)
(Ⅱ)若A=60°,则tanA=$\sqrt{3}$,得tanB=$\frac{\sqrt{3}}{4}$.
∵cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$,
∴$\frac{absinC}{{a}^{2}+{b}^{2}-{c}^{2}}$=$\frac{sinC}{2cosC}=\frac{1}{2}tanC$=-$\frac{1}{2}$tan(A+B)=$\frac{1}{2}×\frac{tanA+tanB}{tanAtanB-1}$=-$\frac{5\sqrt{3}}{2}$.…(12分)
点评 本题主要考查三角函数的恒等变换及化简求值,正弦定理,余弦定理的综合应用,考查了计算能力和转化思想,属于中档题.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案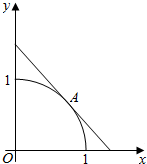 如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )
如图,设圆弧x2+y2=1(x≥0,y≥0)与两坐标轴正半轴围成的扇形区域为M,过圆弧上中点A做该圆的切线与两坐标轴正半轴围成的三角形区域为N.现随机在区域N内投一点B,若设点B落在区域M内的概率为P,则P的值为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
| A. | (-∞,-1)∪(1,+∞) | B. | (-∞,-1]∪[1,+∞) | C. | [-1,1] | D. | (-1,1) |
| A. | 当a>0时,f(x)有零点x0,且x0∈(1,2) | B. | 当a>0时,f(x)有零点x0,且x0∈(2,+∞) | ||
| C. | 当a=0时,f(x)没有零点 | D. | 当a<0时,f(x)有零点x0,且x0∈(2,+∞) |
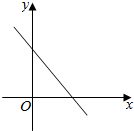
| A. | -$\frac{b}{2a}$>0,$\frac{4ac-{b}^{2}}{4a}$>0 | B. | -$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$>0 | ||
| C. | -$\frac{b}{2a}$>0,$\frac{4ac-{b}^{2}}{4a}$<0 | D. | -$\frac{b}{2a}$<0,$\frac{4ac-{b}^{2}}{4a}$<0 |
| A. | 90 | B. | 80 | C. | 72 | D. | 56 |