题目内容
6.设集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是单元素集合,若存在a<0,b<0使点P∈{(x,y)|(x-a)2+(y-b)2≤1},则点P所在的区域的面积为2π.分析 先根据A∩B是一个单元素集合,得到直线和抛物线相切,得到a2+b2=1,结合图象得到集合P的面积=半径为1小圆的面积+半径为2大圆的面积的$\frac{1}{4}$,问题得以解决
解答 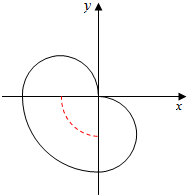 解:集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是一个单元素集合,
解:集合A={(x,y)|y=x2+2bx+1},B={(x,y)|y=2a(x+b)},且A∩B是一个单元素集合,
∴直线和抛物线相切,
∴由x2+2bx+1=2a(x+b),即x2+2(b-a)x+1-2ab=0,有相等的实根,所以△=0即a2+b2=1,
∵存在a<0,b<0,P={(x,y)|(x-a)2+(y-b)2≤1},
∴圆心在以原点为圆心,以1为半径的圆上的一部分(第三象限)
∴如图所示,集合P中圆的边界的移动是半径为1的圆的边界的移动就是沿着那个半径为2的那个$\frac{1}{4}$圆弧上,
∴集合P的面积=半径为1小圆的面积+半径为2大圆的面积的$\frac{1}{4}$,
∴集合C的面积=π+π=2π,
故答案为:2π.
点评 本题考查了直线和抛物线的位置关系,以及集合与集合的关系,关键是画出图形.

练习册系列答案
相关题目
16.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如表:
若抽取学生n人,成绩分为A(优秀),B(良好),C(及格)三个等次,设x,y分别表示数学成绩与地理成绩,例如:表中地理成绩为A等级的共有14+40+10=64(人),数学成绩为B等级且地理成绩为C等级的有8人.已知x与y均为A等级的概率是0.07.
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
| 人数 x y | A | B | C |
| A | 14 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
(Ⅰ)设在该样本中,数学成绩的优秀率是30%,求a,b的值;
(Ⅱ)已知a≥7,b≥6,求数学成绩为A等级的人数比C等级的人数多的概率.
17.已知i是虚数单位,复数z满足(1-i)z=i,则|z|=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
3.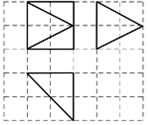 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
 如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )
如图,网格纸上小正方形的边长为a,粗实线画出的是某多面体的三视图,此几何体的表面积为$12+4(\sqrt{2}+\sqrt{5})$,则实数a=( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | 3 |
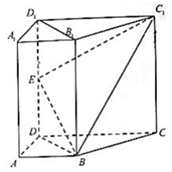 如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.
如图,直四棱柱ABCD-A1B1C1D1中,AB∥CD,AB⊥AD,AD=AB=1.AA1=CD=2.E为棱DD1的中点.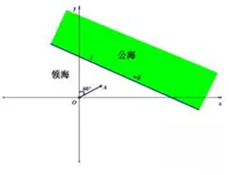 如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.
如图,已知直线l:x+$\sqrt{3}$y-c=0(c>0)为公海与领海的分界线,一艘巡逻艇在O处发现了北偏东60°海面上A处有一艘走私船,走私船正向停泊在公海上接应的走私海轮B航行,以使上海轮后逃窜.已知巡逻艇的航速是走私船航速的2倍,且两者都是沿直线航行,但走私船可能向任一方向逃窜.