题目内容
已知正数x、y满足
,则z=(
)x•(
)y的最小值为( )
|
| 1 |
| 4 |
| 1 |
| 2 |
A、
| |||
B、
| |||
C、2
| |||
| D、4 |
考点:简单线性规划的应用
专题:计算题,作图题,函数的性质及应用,不等式的解法及应用
分析:由题意作出其平面区域,z=(
)x•(
)y=(
)2x+y,令u=2x+y化为y=-2x+u,u相当于直线y=-2x+u的纵截距,由几何意义可得.
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:由题意作出其平面区域,
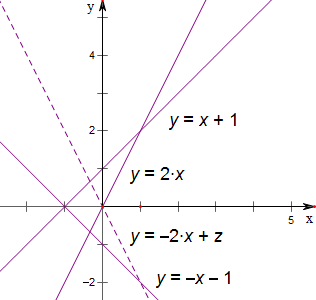
∵z=(
)x•(
)y=(
)2x+y,
∴令u=2x+y化为y=-2x+u,u相当于直线y=-2x+u的纵截距,
∴求z=(
)x•(
)y的最小值可转化为求u的最大值,
由题意知,当x=1,y=2时,u取得最大值4,
故z=(
)x•(
)y的最小值为(
)4=
,
故选A.
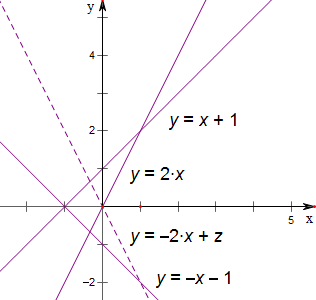
∵z=(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
∴令u=2x+y化为y=-2x+u,u相当于直线y=-2x+u的纵截距,
∴求z=(
| 1 |
| 4 |
| 1 |
| 2 |
由题意知,当x=1,y=2时,u取得最大值4,
故z=(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 16 |
故选A.
点评:本题考查了简单线性规划,作图要细致认真,同时考查了转化的数学思想,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在边长为4的正方形ABCD中,AC与BD相交于O.减去△AOB,将剩下部分沿OC、OD折叠,使OA、OB重合,则以A(B),C,D,O为顶点的四面体的体积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、2
|
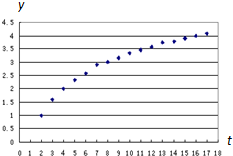 某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )
某研究小组在一项实验中获得一组关于y、t之间的数据,将其整理后得到如图所示的散点图,下列函数中,最能近似刻画y与t之间关系的是( )| A、y=2t |
| B、y=2t2 |
| C、y=log2t |
| D、y=t3 |
对实数a和b,定义运算“*”:a*b=
,设函数f(x)=(x2+1)*(x+2),若函数y=f(x)-c的图象与x轴恰有两个公共点,则实数c的取值范围是( )
|
| A、(1,2]∪(4,5] |
| B、(2,4]∪(5,+∞) |
| C、(-∞,1)∪(4,5] |
| D、[1,2] |