题目内容
在周长为定值的△DEC中,已知|DE|=8,动点C的运动轨迹为曲线G,且当动点C运动时,cosC有最小值-
.
(1)以DE所在直线为x轴,线段DE的中垂线为y轴建立直角坐标系,求曲线G的方程;
(2)直线l分别切椭圆G与圆M:x2+y2=R2(其中3<R<5)于A、B两点,求|AB|的范围.
| 7 |
| 25 |
(1)以DE所在直线为x轴,线段DE的中垂线为y轴建立直角坐标系,求曲线G的方程;
(2)直线l分别切椭圆G与圆M:x2+y2=R2(其中3<R<5)于A、B两点,求|AB|的范围.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)设|CD|+|CE|=2a(a>4)为定值,则C点的轨迹是以D、E为焦点的椭圆,焦距2c=|DE|=8.再由cosC有最小值-
,推导出a2=25.由此能求出C点轨迹G的方程.
(2)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,直线AB的方程为:y=kx+m,有
,得(25k2+9)x2+50kmx+25(m2-9)=0,由此利用相切的性质能求出|AB|的范围.
| 7 |
| 25 |
(2)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,直线AB的方程为:y=kx+m,有
|
解答:
解:(1)由题意设|CD|+|CE|=2a(a>4)为定值,
∴C点的轨迹是以D、E为焦点的椭圆,∴焦距2c=|DE|=8.…..(2分)
∵cosC=
=
=
-1,
又|CD|•|CE|≤(
)2=a2,∴cosC≥1-
,….(4分)
由题意得1-
=-
,∴a2=25.
∴C点轨迹G的方程为
+
=1,x≠±5…..(6分)
(2)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,
直线AB的方程为:y=kx+m,∵A既在椭圆上,又在直线AB上,
∴
,…..(8分)
消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,
由于直线与椭圆相切,故△=(50km)2-4(25k2+9)×25(m2-9)=0,
从而可得:m2=9+25k2,①,x1=-
②….(10分)
由
,消去y得:(k2+1)x2+2kmx+m2-R2=0.
由于直线与圆相切,得:m2=R2(1+k2),③,x2=-
,④
由②④得:x2-x1=
;由①③得:k2=
,
∴|AB|2=(x2-x1)2+(y2-y1)2=(1+k2)(x2-x1)2
=
•
=
•
=25+9-R2-
,
∵3<R<5,∴30≤R2+
<34,
∴0<|AB|2≤4,∴0<|AB|≤2,
∴|AB|的范围是(0,2].….(14分)
∴C点的轨迹是以D、E为焦点的椭圆,∴焦距2c=|DE|=8.…..(2分)
∵cosC=
| |CD|2+|CE|2-82 |
| 2|CD||CE| |
=
| (|CD|+|CE|)2-2|CD||CE|-64 |
| 2|CD||CE| |
=
| 2a2-32 |
| |CD||CE| |
又|CD|•|CE|≤(
| 2a |
| 2 |
| 32 |
| a2 |
由题意得1-
| 32 |
| a2 |
| 7 |
| 25 |
∴C点轨迹G的方程为
| x2 |
| 25 |
| y2 |
| 9 |
(2)设A(x1,y1),B(x2,y2)分别为直线l与椭圆和圆的切点,
直线AB的方程为:y=kx+m,∵A既在椭圆上,又在直线AB上,
∴
|
消去y得:(25k2+9)x2+50kmx+25(m2-9)=0,
由于直线与椭圆相切,故△=(50km)2-4(25k2+9)×25(m2-9)=0,
从而可得:m2=9+25k2,①,x1=-
| 25k |
| m |
由
|
由于直线与圆相切,得:m2=R2(1+k2),③,x2=-
| kR2 |
| m |
由②④得:x2-x1=
| k(25-R2) |
| m |
| R2-9 |
| 25-R2 |
∴|AB|2=(x2-x1)2+(y2-y1)2=(1+k2)(x2-x1)2
=
| m2 |
| R2 |
| k2(25-R2) |
| m2 |
| R2-9 |
| R2 |
| (25-R2)2 |
| 25-R2 |
| 225 |
| R2 |
∵3<R<5,∴30≤R2+
| 225 |
| R2 |
∴0<|AB|2≤4,∴0<|AB|≤2,
∴|AB|的范围是(0,2].….(14分)
点评:本题考查曲线的方程的求法,考查线段长的取值范围的求法,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
取一根长度为4米的绳子,拉直后在任意位置剪断,那么剪得的两段都不少于1米的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
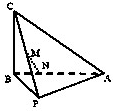 如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB.
如图,在三棱锥C-PAB中,AB⊥BC,PB⊥BC,PA=PB=5,AB=6,BC=4,点M是PC的中点,点N在线段AB上,且MN⊥AB. 如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.
如图所示,△ABC是圆O的内接三角形,AC=BC,D为弧AB上任一点,延长DA至点E,使CE=CD.