Question

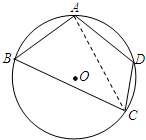某市某棚户区改造建筑用地平面示意图如图所示．经规划调研确定，棚改规划建筑用地区域是半径为R的圆面．该圆面的内接四边形ABCD是原棚户建筑用地，测量可知边界AB=AD=4千米，BC=6千米，CD=2千米，
（1）求原棚户区建筑用地ABCD中对角线AC的长度；
（2）请计算原棚户区建筑用地ABCD的面积及圆面的半径R的值．

Answer 1

考点：余弦定理,正弦定理

专题：三角函数的求值

分析：（1）连接AC，由四边形ABCD为圆内接四边形，利用圆内接四边形对角互补得到∠ABC+∠ADC=180°，在三角形ABC与三角形ADC中，分别利用余弦定理表示出AC²，将各自的值代入求出cos∠ABC的值，进而确定出∠ABC与∠ADC的度数，代入计算即可求出AC的长；
（2）四边形ABCD面积=三角形ABC面积+三角形ADC面积，求出即可；在三角形ABC中，利用正弦定理即可求出R的值．

解答： 解：（1）连接AC，
∵四边形ABCD为圆的内接四边形，
∴∠ABC+∠ADC=180°，
∵AB=AD=4千米，BC=6千米，CD=2千米，
∴由余弦定理得：AC²=4²+6²-2×4×6cos∠ABC=4²+2²-2×2×4cos∠ADC，
∴cos∠ABC=

1

2

，
∵∠ABC为三角形内角，
∴∠ABC=60°，∠ADC=120°，
∴AC²=4²+6²-2×4×6×

1

2

=28，即AC=2

7

（千米）；
（2）根据题意得：S_{四边形ABCD}=

1

2

×4×6sin60°+

1

2

×2×4sin120°=8

3

（平方千米），
由正弦定理得：2R=

AC

sinB

=

2 7

3 2

=

4 21

3

（千米），
则R=

2 21

3

（千米）．

点评：此题考查了正弦、余弦定理，以及特殊角的三角函数值，熟练掌握定理是解本题的关键．