题目内容
写出终边在直线上角的集合y=
x上角的集合 .
| 3 |
考点:终边相同的角
专题:三角函数的求值
分析:由终边相同的角的定义,先写出终边落在射线y=
x(x≥0)的角的集合,再写出终边落在射线y=
x (x≤0)的角的集合,最后求两个集合的并集即可.
| 3 |
| 3 |
解答:
解:由终边相同的角的定义,终边落在射线y=
x (x≥0)的角的集合为{α|α=
+2kπ,k∈Z}
终边落在射线y=-x (x≤0)的角的集合为{α|α=
+2kπ,k∈Z}={α|α=
+π+2kπ,k∈Z}
={α|α=
+(2k+1)π,k∈Z}
∴终边落在直线y=-x的角的集合为{α|α=
+2kπ,k∈Z}∪{α|α=
+(2k+1)π,k∈Z}={α|α=
+kπ,k∈Z}
故答案为:{α|α=kπ+
,k∈Z}.
| 3 |
| π |
| 3 |
终边落在射线y=-x (x≤0)的角的集合为{α|α=
| 4π |
| 3 |
| π |
| 3 |
={α|α=
| π |
| 3 |
∴终边落在直线y=-x的角的集合为{α|α=
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
故答案为:{α|α=kπ+
| π |
| 3 |
点评:本题考查了终边相同的角的定义和表示方法,解题时要区分终边落在射线上和落在直线上的不同,求并集时要注意变形.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
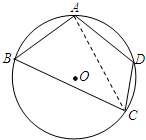 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米, 如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为
如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为