题目内容
三棱锥P-ABC是侧棱长为2的正三棱锥,△ABC是底面,PA⊥PB,此三棱锥的四个顶点都在同一球面上,则该球的体积为 .
考点:球的体积和表面积
专题:球
分析:判断正三棱锥的形状,三棱锥扩展为正方体,三棱锥与正方体的外接球相同,求出外接球的半径即可求解球的体积.
解答:
解:三棱锥P-ABC是侧棱长为2的正三棱锥,△ABC是底面,PA⊥PB,
∴PA⊥PC,PC⊥PB,
三棱锥是正方体的一个角,三棱锥扩展为正方体,
正三棱锥的外接球与正方体的外接球相同,正方体的棱长为:2,
正方体的对角线计算外接球的直径,球的半径为:
×2
=
.
该球的体积为:
r3=4
π.
故答案为:4
π.
∴PA⊥PC,PC⊥PB,
三棱锥是正方体的一个角,三棱锥扩展为正方体,
正三棱锥的外接球与正方体的外接球相同,正方体的棱长为:2,
正方体的对角线计算外接球的直径,球的半径为:
| 1 |
| 2 |
| 3 |
| 3 |
该球的体积为:
| 4π |
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题考查几何体的外接球以及球的体积的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
等比数列{an}满足a2+a4=20,a3+a5=40,则公比q=( )
A、
| ||
B、-
| ||
| C、2 | ||
| D、-2 |
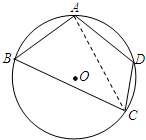 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,