题目内容
△ABC的三个内角A、B、C所对的边分别为a、b、c,若bcosA=
a,则
的取值范围为 .
| 2 |
| a |
| c |
考点:正弦定理,余弦定理
专题:解三角形
分析:利用正弦定理把已知等式中的边换成角的正弦化简后,代入sinC的表达式,进而根据正弦定理把
的范围,转化为
的范围,利用cosB的有界性求得答案.
| a |
| c |
| sinA |
| sinC |
解答:
解:△ABC中,根据正弦定理
=
=
知,
=
,
∵bcosA=
a,
∴sinBcosA=
sinA,
又∵sinC=sin(A+B)=sinAcosB+sinBcosA=sinAcosB+
sinA,
∴
=
=
=
,
∵∠B∈(0,π),
∴-1<cosB<1,
∴
-1<cosB+
<1+
,
∴
>
>
,
∴
-1<
<
+1,
故答案为:(
-1,
+1).
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
| a |
| c |
| sinA |
| sinC |
∵bcosA=
| 2 |
∴sinBcosA=
| 2 |
又∵sinC=sin(A+B)=sinAcosB+sinBcosA=sinAcosB+
| 2 |
∴
| a |
| c |
| sinA |
| sinC |
| sinA | ||
sinAsinB+
|
| 1 | ||
cosB+
|
∵∠B∈(0,π),
∴-1<cosB<1,
∴
| 2 |
| 2 |
| 2 |
∴
| 1 | ||
|
| 1 | ||
cosB+
|
| 1 | ||
|
∴
| 2 |
| a |
| c |
| 2 |
故答案为:(
| 2 |
| 2 |
点评:本题主要考查了正弦定理的运用.在涉及三角形中范围的问题,往往需要利用正弦定理转化成角的问题,进而利用三角函数的性质解决问题.

练习册系列答案
相关题目
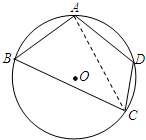 某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米,
某市某棚户区改造建筑用地平面示意图如图所示.经规划调研确定,棚改规划建筑用地区域是半径为R的圆面.该圆面的内接四边形ABCD是原棚户建筑用地,测量可知边界AB=AD=4千米,BC=6千米,CD=2千米, 如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为
如图矩形长为5,宽为2,在矩形内随机地撒200颗黄豆,数得落在阴影部分的黄豆数为120颗,则我们可以估计出阴影部分的面积为