题目内容
某化工厂生产的某种化工产品,当年产量在150吨至250吨之间时,其生产的总成本y(万元)与年产量(吨)之间的函数关系式近似地表示为y=
-30x+4000.问:
(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
(2)年产量为多少吨时,每吨的平均成本最低?并求出最低成.
| x2 |
| 10 |
(1)每吨平均出厂价为16万元,年产量为多少吨时,可获得最大利润?并求出最大利润;
(2)年产量为多少吨时,每吨的平均成本最低?并求出最低成.
考点:基本不等式在最值问题中的应用
专题:应用题,不等式的解法及应用
分析:(1)根据题意得出z=16x-(
-30x+4000)=-
+46x-4000=-
(x-230)2+1290,(150≤x≤250),利用二次函数求解即可.
(2)得出函数式子W=
=
-30=
(x+
)-30,(150≤x≤250),运用基本不等式求解即可.
| x2 |
| 10 |
| x2 |
| 10 |
| 1 |
| 10 |
(2)得出函数式子W=
| y |
| x |
| x |
| 10 |
| 4000 |
| x |
| 1 |
| 10 |
| 40000 |
| x |
解答:
解:(1)年产量为x,年利润为z万元,根据题意得:
z=16x-(
-30x+4000)=-
+46x-4000
=-
(x-230)2+1290,(150≤x≤250),
当x=230时,y大=1290(万元),
(2)年产量为x吨时,每吨的平均成本为W万元,为y=
-30x+4000.
∴W=
=
-30=
(x+
)-30,(150≤x≤250),
∵x+
≥2
=400,(x=200等号成立),
∴x=200时,W最小=
×400-30=10.
故年产量为200吨时,每吨的平均成本最低为10万元.
z=16x-(
| x2 |
| 10 |
| x2 |
| 10 |
=-
| 1 |
| 10 |
当x=230时,y大=1290(万元),
(2)年产量为x吨时,每吨的平均成本为W万元,为y=
| x2 |
| 10 |
∴W=
| y |
| x |
| x |
| 10 |
| 4000 |
| x |
| 1 |
| 10 |
| 40000 |
| x |
∵x+
| 40000 |
| x |
| 40000 |
∴x=200时,W最小=
| 1 |
| 10 |
故年产量为200吨时,每吨的平均成本最低为10万元.
点评:本题考查了函数,基本不等式在实际问题中的应用,属于中档题.

练习册系列答案
相关题目
已知向量
=(1,2),
=(k+1,1),若
⊥
,则k=( )
| a |
| b |
| a |
| b |
| A、3 | B、-3 | C、2 | D、-2 |
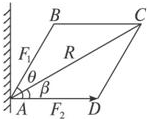 如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.
如图所示,支座A受F1,F2两个力的作用,已知|F1|=45N,与水平线成θ角,|F2|=20N,沿水平方向,两个力的合力|F|=50N,求角θ以及合力F与水平线夹角的夹角β.