题目内容
已知点F(1,0),直线l:x=-1,点P在直线l上运动,PQ⊥l,线段PF与y轴的交点为R,且
•
=0.
(1)求动点Q的轨迹C的方程
(2)直线l与x轴交于点M,过F的直线l1交轨迹C于A,B两点,试探究点M与以AB为直径的圆的位置关系,并加以说明.
| RQ |
| FP |
(1)求动点Q的轨迹C的方程
(2)直线l与x轴交于点M,过F的直线l1交轨迹C于A,B两点,试探究点M与以AB为直径的圆的位置关系,并加以说明.
考点:轨迹方程,直线与圆的位置关系
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由已知条件知,点R是线段FP的中点,RQ是线段FP的垂直平分线,点Q的轨迹E是以F为焦点,l为准线的抛物线,写出抛物线标准方程.
(2)分类讨论,求出|MN|与半径,即可得出结论.
(2)分类讨论,求出|MN|与半径,即可得出结论.
解答:
解:(1)依题意知,直线l的方程为:x=-1,设直线l与x轴交于点K(-1,0),由OK平行于直线l可得,
OR是△FPK的中位线,故点R是线段FP的中点.
又RQ⊥FP,∴RQ是线段FP的垂直平分线.∴|PQ|是点Q到直线l的距离.
∵点Q在线段FP的垂直平分线,∴|PQ|=|QF|.
故动点Q的轨迹E是以F为焦点,l为准线的抛物线,其方程为:y2=4x.
(2)①AB⊥x轴时,以AB为直径的圆的方程为(x-1)2+y2=4,M(-1,0)在圆上;
②AB斜率存在时,设方程为y=k(x-1),A(x1,y1),B(x2,y2),
直线代入抛物线可得k2x2-(4+2k2)x+k2=0,
∴x1+x2=2+
,x1x2=1,
圆的直径|AB|=x1+x2+p=4+
,AB中点(1+
,
),
∴|MN|=
>
=2+
=
|AB|,
∴M(-1,0)在圆外.
OR是△FPK的中位线,故点R是线段FP的中点.
又RQ⊥FP,∴RQ是线段FP的垂直平分线.∴|PQ|是点Q到直线l的距离.
∵点Q在线段FP的垂直平分线,∴|PQ|=|QF|.
故动点Q的轨迹E是以F为焦点,l为准线的抛物线,其方程为:y2=4x.
(2)①AB⊥x轴时,以AB为直径的圆的方程为(x-1)2+y2=4,M(-1,0)在圆上;
②AB斜率存在时,设方程为y=k(x-1),A(x1,y1),B(x2,y2),
直线代入抛物线可得k2x2-(4+2k2)x+k2=0,
∴x1+x2=2+
| 4 |
| k2 |
圆的直径|AB|=x1+x2+p=4+
| 4 |
| k2 |
| 2 |
| k2 |
| 2 |
| k |
∴|MN|=
(1+
|
4+
|
| 2 |
| k2 |
| 1 |
| 2 |
∴M(-1,0)在圆外.
点评:本题考查轨迹方程的求法、抛物线的定义、标准方程,以及简单性质的应用,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
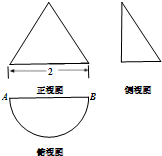 一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为
一个几何体的三视图如图所示,其中正视图是等边三角形,俯视图是半圆.现有一只蚂蚁从点A出发沿该几何体的侧面环绕一周回到A点,则蚂蚁所经过路程的最小值为 如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是
如图,一个广告气球被一束入射角为30°的平行光线照射,其投影是一个最长的弦长为5米的椭圆,则制作这个广告气球至少需要的面料是