题目内容
某市有M,N,S三所高校,其学生会学习部有“干事”人数分别为36,24,12,现采用分层抽样的方法从这些“干事”中抽取6名进行“大学生学习部活动现状”调查.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
(Ⅰ)求应从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)若从抽取的6名干事中随机选2,求选出的2名干事来自同一所高校的概率.
考点:古典概型及其概率计算公式,分层抽样方法
专题:概率与统计
分析:(Ⅰ)求出抽样比,即可从M,N,S这三所高校中分别抽取的“干事”人数;
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,来自高校N的2名分别记为a、b,来自高校S的1名记为c,写出选出2名干事的所有可能结果,设A={所选2名干事来自同一高校},写出事件A的所有可能结果,利用古典概型求解即可.
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,来自高校N的2名分别记为a、b,来自高校S的1名记为c,写出选出2名干事的所有可能结果,设A={所选2名干事来自同一高校},写出事件A的所有可能结果,利用古典概型求解即可.
解答:
解:(Ⅰ)抽样比为:
=
,
故应从M,N,S这三所高校抽取的“干事”人数分别为3,2,1;
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,
来自高校N的2名分别记为a、b,来自高校S的1名记为c,
则选出2名干事的所有可能结果为:
{1,2},{1,3},{1,a },{1,b },{1,c},
{2,3},{2,a},{2,b},{2,c},
{3,a},{3,b },{3,c },
{ a,b },{ a,c },
{ b,c}共15种.
设A={所选2名干事来自同一高校},
事件A的所有可能结果为{1,2},{1,3},{2,3},{a,b},共4种,
所以P(A)=
.
| 6 |
| 36+24+12 |
| 1 |
| 12 |
故应从M,N,S这三所高校抽取的“干事”人数分别为3,2,1;
(Ⅱ)在抽取到的6名干事中,来自高校M的3名分别记为1、2、3,
来自高校N的2名分别记为a、b,来自高校S的1名记为c,
则选出2名干事的所有可能结果为:
{1,2},{1,3},{1,a },{1,b },{1,c},
{2,3},{2,a},{2,b},{2,c},
{3,a},{3,b },{3,c },
{ a,b },{ a,c },
{ b,c}共15种.
设A={所选2名干事来自同一高校},
事件A的所有可能结果为{1,2},{1,3},{2,3},{a,b},共4种,
所以P(A)=
| 4 |
| 15 |
点评:本题考查古典概型的应用,分层抽样,基本知识的考查,是高考文科概率考试类型题目.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
已知命题p:?x∈R,x-2>0,命题q:?x∈R,
>x,则下列说法中正确的是( )
| x |
| A、命题p∨q是假命题 |
| B、命题p∧q是真命题 |
| C、命题p∨(¬q)是假命题 |
| D、命题p∧(¬q)是真命题 |

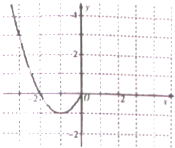 已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)图象是抛物线的一部分(如图所示).
已知函数f(x)是定义在R上的偶函数,且当x≤0时,f(x)图象是抛物线的一部分(如图所示).