题目内容
1.如图,在长方体ABCD-A1B1C1D1中,E,F分别为A1B1,A1D1的中点,求证:DF∥平面ACE.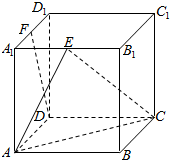
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能证明DF∥平面ACE.
解答 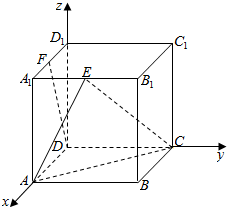 证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
证明:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
在长方体ABCD-A1B1C1D1中,设AB=a,AD=b,AA1=c,
∵E,F分别为AB1,A1D1的中点,
∴D(0,0,0),F($\frac{a}{2}$,0,c),A(a,0,0),C(0,b,0),E(a,$\frac{b}{2}$,c),
$\overrightarrow{DF}$=($\frac{a}{2}$,0,c),$\overrightarrow{AC}$=(-a,b,0),$\overrightarrow{AE}$=(0,$\frac{b}{2}$,c),
设平面ACE的法向量$\overrightarrow{n}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=-ax+by=0}\\{\overrightarrow{n}•\overrightarrow{AE}=\frac{b}{2}y+cz=0}\end{array}\right.$,取x=1,得$\overrightarrow{n}$=(1,$\frac{a}{b}$,-$\frac{a}{2c}$),
$\overrightarrow{DF}•\overrightarrow{n}$=$\frac{a}{2}-\frac{a}{2}$=0,
∵DF?平面ACE,∴DF∥平面ACE.
点评 本题考查线面平行的证明,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.对于任意实数a、b∈[0,1],则a、b满足a<b<$\sqrt{a}$的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{7}$ |
9.设a,b,c为三角形ABC三边,a≠1,b<c,若logc+ba+logc-ba=2logc+balog c-ba,则三角形ABC的形状为( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 无法确定 |
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )
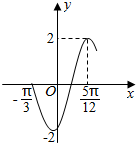
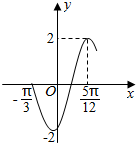
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
6.下列命题正确的是( )
| A. | 空间中两直线所成角的取值范围是:0°<θ≤90° | |
| B. | 直线与平面所成角的取值范围是:0°≤θ≤90° | |
| C. | 直线倾斜角的取值范围是:0°<θ≤180° | |
| D. | 两异面直线所成的角的取值范围是:0°<θ<90° |