题目内容
16.函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则( )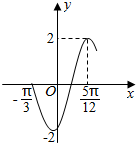
| A. | 函数f(x)的最小正周期是2π | |
| B. | 函数f(x)的图象可由函数g(x)=2sin2x的图象向右平移$\frac{π}{3}$个单位长度得到 | |
| C. | 函数f(x)的图象关于直线x=-$\frac{π}{12}$对称 | |
| D. | 函数f(x)在区间[-$\frac{7π}{12}$+kπ,-$\frac{π}{12}$+kπ](k∈Z)上是增函数 |
分析 根据图象的两个点A、B的横坐标,得到四分之三个周期的值,得到周期的值,做出ω的值,把图象所过的一个点的坐标代入方程做出初相,写出解析式,利用正弦函数的图象和性质即可得解.
解答 解:由图象可以看出正弦函数的四分之三个周期是$\frac{5π}{12}$-(-$\frac{π}{3}$)=$\frac{3π}{4}$,
∴T=$\frac{2π}{ω}$=π,故A不正确;
∴ω=2,
又由函数f(x)的图象经过($\frac{5π}{12}$,2)
∴2=2sin(2×$\frac{5π}{12}$+φ)
∴$\frac{5π}{6}$+φ=2kπ+$\frac{π}{2}$,(k∈Z),
即φ=2kπ-$\frac{π}{3}$
又由-$\frac{π}{2}$<φ<$\frac{π}{2}$,则φ=-$\frac{π}{3}$,
∴函数解析式为:f(x)=2sin(2x-$\frac{π}{3}$).
由g(x-$\frac{π}{3}$)=2sin2(x-$\frac{π}{3}$)=2sin(2x-$\frac{2π}{3}$)≠f(x),故B不正确;
由f(-$\frac{π}{12}$)=2sin[2×(-$\frac{π}{12}$)-$\frac{π}{3}$]=-2,故C正确;
由2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$,k∈Z,即可解得单调递增区间为:[-$\frac{π}{12}$+kπ.kπ+$\frac{5π}{12}$],k∈Z,故D不正确;
故选:C.
点评 本题考查有部分图象确定函数的解析式,考查了正弦函数的图象和性质,本题解题的关键是确定初相的值,这里利用代入点的坐标求出初相.属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | 4条 | B. | 3条 | C. | 2条 | D. | 1条 |
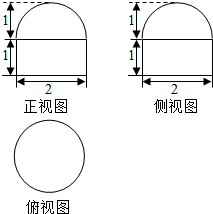 已知一个空间组合体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,请说出该组合体由哪些几何体组成,并且求出该组合体的表面积和体积.
已知一个空间组合体的三视图如图所示,其中正视图、侧视图都是由半圆和矩形组成,请说出该组合体由哪些几何体组成,并且求出该组合体的表面积和体积.