题目内容
15．已知某几何体的正视图和侧视图均如图所示，给出下列5个图形：
其中可以作为该几何体的俯视图的图形个数是（ ）
| A． | 5个 | B． | 4个 | C． | 3个 | D． | 2个 |
分析 由三视图的定义，结合正视图与侧视图的图形相同，对题目中的图形进行分析，即可得出结论．
解答 解：对于④中的图形，中间是正三角形，它在正视图与侧视图中矩形宽度不一致，
所以④不能作为该几何体的俯视图图形；
对于其他图形，中间图形的正视图与侧视图的矩形宽度一致，可以作为该几何体的俯视图图形．
所以，满足条件的图形个数有①②③⑤共4个．
故选：B．
点评 本题考查了空间中三视图的应用问题，是基础题目．
练习册系列答案
相关题目
3．已知命题p：关于x的函数y=x2-3ax+4在[1，+∞）上是增函数，命题q：关于x的函数y=（2a-1）x在[1，+∞）上是减函数．若“p且q”为真命题，则实数a的取值范围是（ ）
| A． | （-∞，$\frac{2}{3}$] | B． | （0，$\frac{1}{2}$） | C． | （$\frac{1}{2}$，$\frac{2}{3}$] | D． | （$\frac{1}{2}$，1） |
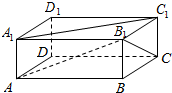如图所示，ABCD-A1B1C1D1是长方体，AA1=a，∠BAB1=∠B1A1C1=30°，则AB与A1C1所成的角为30°，AA1与B1C所成的角为45°．
如图，在△ABC中，BC边上的中线AD长为3，且BD=2，$sinB=\frac{{3\sqrt{6}}}{8}$．
4．${x^2}-{log_a}（x+1）＜2x-1在（\frac{1}{2}，1）$内恒成立，则a的取值范围是（ ）
| A． | $[{（{\frac{3}{2}}）^{-4}}，1）$ | B． | $（{（{\frac{3}{2}}）^{-4}}，1）$ | C． | $（1，{（{\frac{3}{2}}）^4}）$ | D． | $（1，{（{\frac{3}{2}}）^4}]$ |